ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1.1. Методы расчёта показателей надёжности

Критериями надёжности невосстанавливаемых систем являются:

- P_c(t) – вероятность безотказной работы системы в течении времени t;

- Q_c(t) – вероятность отказа системы в течении времени t;

- T_c – среднее время безотказной работы системы;

- λ_с(t) – интенсивность отказов системы в момент t;

- f_c(t) – плотность распределения времени до отказа.

Между этими показателями существуют следующие зависимости:

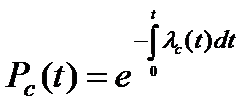,	(1)
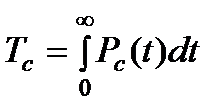,	(2)
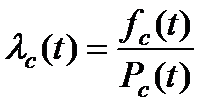,	(3)
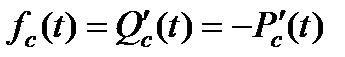,	(4)
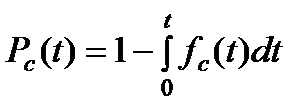.	(5)

Следует иметь в виду, что среднее время безотказной работы является неудовлетворительным показателем надёжности систем с коротким временем работы.

Нерезервированной называется такая система, в которой отказ любого элемента приводит отказу всей системы. При этом остальные элементы системы прекращают свою работу.

Показатели надёжности нерезервированной системы, состоящей из n элементов, вычисляются по формулам:

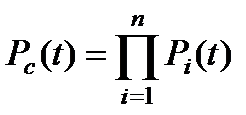,	(6)
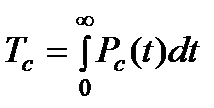,	(7)
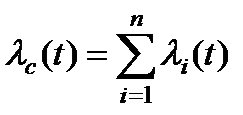,	(8)
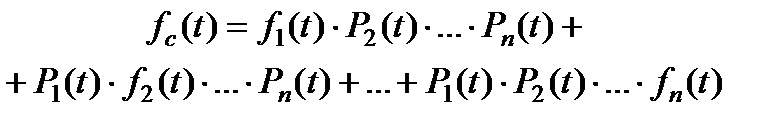,	(9)

где P_i(t) – вероятность безотказной работы i-го элемента, i = 1, 2, …, n;

f_i(t) – плотность распределения времени до отказа i-го элемента, i = 1, 2, …, n;

λ_i(t) – интенсивность отказов i-го элемента, i = 1, 2, …, n.

Существует другой способ вычисления плотности распределения времени до отказа системы, его рекомендуется использовать в качестве проверочного:

.

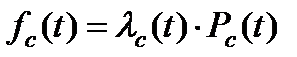Среднее время безотказной работы системы также может быть определено по формуле Симпсона. Для системы из пяти элементов формула Симпсона принимает вид:

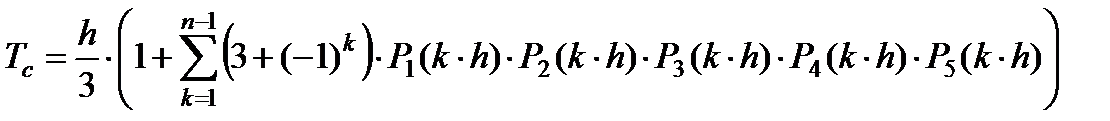где n– число точек,

h– шаг интегрирования, выбираемый из условия обеспечения требуемой точности.

Для случая постоянных интенсивностей отказов элементов имеют место соотношения:

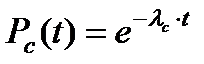,	(10)
,	(11)
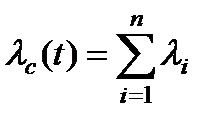,	(12)
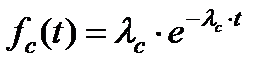.	(13)

1.2. Законы распределения времени работы до отказа

Время работы элементов до отказа является случайной величиной и может подчиняться одному из законов распределения. Каждый закон характеризуется параметрами распределения (они указаны в скобках после условного обозначения закона):

- Вейбулла - W(α, β);

- гамма - Г(α, β);

- Рэлея - R(λ);

- экспоненциальный - Exp(λ);

- усечённый нормальный - TN(m₀, σ₀);

- нормальный – N(m, σ);

- равномерный – U(a, b).

Таблица 1

Связь параметров распределений с начальными моментами

Распределение	m	σ
Экспоненциальное Exp(λ)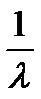
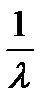
Равномерное U(a, b), a ≥ 0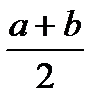
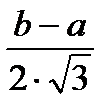
Гамма Г(α, β)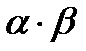
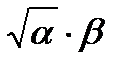
Усечённое нормальное TN(m0, σ0)		, ,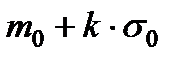
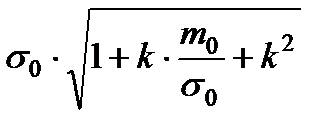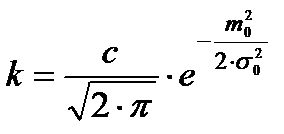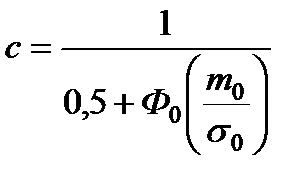
Рэлея R(λ)
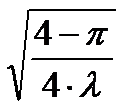
Вейбулла W(α, β)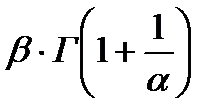
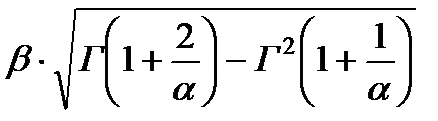
Нормальное N(m, σ) m > 3∙σ	m	σ

Для всех законов существуют начальные моменты распределений: математическое ожидание и среднее квадратическое отклонение. Связь начальных моментов с параметрами распределений приведена в табл. 1.

Таблица 2

Связь параметров распределений вероятностью безотказной работы и плотностью распределения времени до отказа

Распределение	f(t)	P(t)
Экспоненциальное Exp(λ)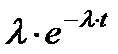
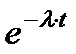
Равномерное U(a, b), a ≥ 0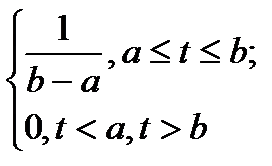
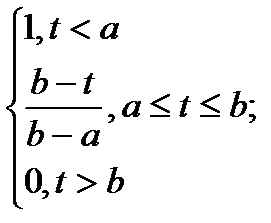
Гамма Г(α, β)
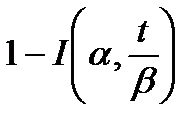
Усечённое нормальное TN(m0, σ0) m ≥ 1,33∙σ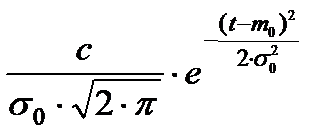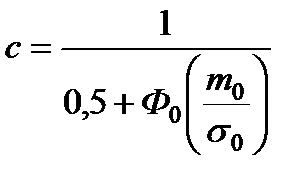
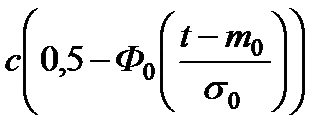
Рэлея R(λ)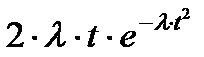
Вейбулла W(α, β)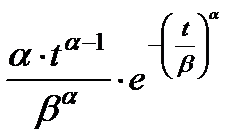
Нормальное N(m, σ), m > 3∙σ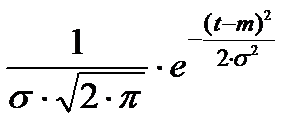

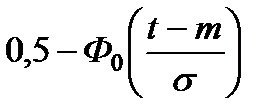
В таблицах 1 и 2 введены следующие обозначения:

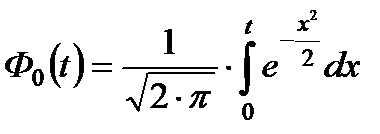- функция Лапласа;

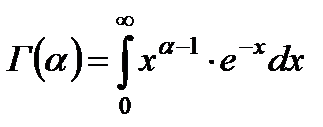- гамма-функция;

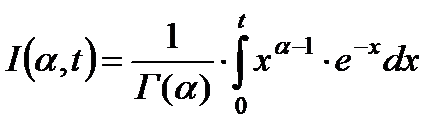- неполная гамма-функция.

Простым способом вычисления значений этих функций является обращение к системе Microsoft Excel.

Для вычисления вероятности безотказной работы и плотности распределения времени до отказа используются аналитические выражения, которые приведены в табл. 2.

Дата добавления: 2014-10-17; просмотров: 291; Нарушение авторских прав

Мы поможем в написании ваших работ!