
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
Нерезервированная система состоит из пяти элементов, имеющих различные законы распределения времени работы до отказа. Виды законов распределения и их параметры приведены в табл. 3
Таблица 3
Законы распределения времени до отказа элементов и их параметры
| Элементы | ||||
| TN(390; 100) | Г(9; 65) | Exp(8·10-5) | R(2·10-5) | W(5; 200) |
Определить показатели надёжности каждого элемента и всей системы:
- вероятность безотказной работы;
- среднее время безотказной работы;
- интенсивность отказов;
- плотность распределения времени безотказной работы.
Для показателей, зависящих от времени, получить решение в виде графиков и таблиц.
Поскольку решение данной задачи сопряжено с большим объёмом однотипных вычислений, необходимо воспользоваться системой Microsoft Excel. Это позволит существенно сократить время решения задачи и избежать технических ошибок при проведении вычислений.
Для расчёта показателей, зависящих от времени (вероятности безотказной работы, плотности распределения времени безотказной работы и интенсивности отказов), необходимо создать таблицы, в левом столбце которых расположить ряд значений времени t, для каждого из которых эти показатели будут вычислены. Шаг рекомендуется выбрать таким, чтобы получилось минимум 10 отличных от нуля значений показателей надёжности.
Затем для каждого показателя надёжности создаётся массив данных по каждому элементу (табл. 4-6).
Для большинства заданных законов в системе Microsoft Excel имеются статистические функции, которые могут быть интегрированы в ячейки таблицы при помощи мастера функций.
Нормальное распределение
Функция НОРМРАСП. Возвращает нормальную функцию распределения: НОРМРАСП(x;среднее;стандартное_откл;интегральная). Здесь в качестве аргумента «х» следует указать ссылку на ячейку со значением времени t; вместо «среднее» записать значение m (в нашем примере m = 390); вместо «стандартное_откл» - значение σ (в нашем примере σ = 100). Для расчёта вероятности отказа вместо «интегральная» следует вписать значение ИСТИНА, для расчёта плотности распределения принимается значение ЛОЖЬ. Следует обратить внимание, что данная функция возвращает вероятность отказа Q(t), поэтому для вычисления вероятности безотказной работы следует воспользоваться формулой: P(t) = 1 - Q(t).
Усечённое нормальное распределение
Для расчёта показателей надёжности также используется функция НОРМРАСП. Однако, вычисленные с её помощью значения P(t) и f(t) следует умножить на коэффициент с (см. табл. 2). Этот коэффициент зависит от функции Лапласа Ф0(m0/σ0), которая вычисляется следующим образом: НОРМРАСП(x;0;1;ИСТИНА) – 0,5. Здесь в качестве аргумента «х» следует ввести отношение m0/σ0 (в нашем примере m0/σ0 = 390/100 = 3,9).
Гамма-распределение
Функция ГАММАРАСП. Возвращает гамма-распределение: ГАММАРАСП(x;альфа ;бета ;интегральная). Аргументы подставляются аналогично нормальному распределению: в качестве аргумента «х» выступает время t; α и β – параметры распределения (в нашем примере α = 9, β = 65). При подстановке значения ИСТИНА функция определяет вероятность отказа, по которой следует определить вероятность безотказной работы.
Экспоненциальное распределение
Функция ЭКСПРАСП. Возвращает экспоненциальное распределение: ЭКСПРАСП(x;лямбда;интегральная). Аргументы подставляются аналогично предыдущим функциям (в нашем примере λ = 8∙10-5). Со значение ИСТИНА функция вычисляет вероятность отказа. Также данную функцию можно записать вручную в виде формулы (см. табл. 2).
Распределение Рэлея
Данную функцию также можно записать вручную ввиду её простоты. Другой способ – воспользоваться функцией ЭКСПРАСП(x;лямбда;интегральная), однако в качестве аргумента «х» записывать значение t2 (в нашем примере параметр распределения λ = 2∙10-5), а также при вычислении f(t) умножить полученное с помощью ЭКСПРАСП значение на 2∙t.
Распределение Вейбулла
Функция ВЕЙБУЛЛ. Возвращает распределение Вейбулла: ВЕЙБУЛЛ(x;альфа;бета;интегральная). При записи вместо «интегральная» значения ИСТИНА вычисляется вероятность отказа (в нашем примере α = 5, β = 200).
Интенсивность отказов для любого закона распределения вычисляется по формуле (3).
Таблица 4
Вероятности безотказной работы элементов и системы
| Время t | Элементы | Система | ||||
| TN(390; 100) | Г(9; 65) | Exp(8·10-5) | R(2·10-5) | W(5; 200) | ||
| 1,0E+00 | 1,0E+00 | 1,0E+00 | 1,0E+00 | 1,0E+00 | 1,0E+00 | |
| 1,0E+00 | 1,0E+00 | 9,9E-01 | 8,2E-01 | 9,7E-01 | 7,9E-01 | |
| 9,7E-01 | 1,0E+00 | 9,8E-01 | 4,5E-01 | 3,7E-01 | 1,6E-01 | |
| 8,2E-01 | 9,5E-01 | 9,8E-01 | 1,7E-01 | 5,0E-04 | 6,3E-05 | |
| 4,6E-01 | 8,3E-01 | 9,7E-01 | 4,1E-02 | 1,3E-14 | 1,9E-16 | |
| 1,4E-01 | 6,4E-01 | 9,6E-01 | 6,7E-03 | 0,0E+00 | 0,0E+00 | |
| 1,8E-02 | 4,3E-01 | 9,5E-01 | 7,5E-04 | 0,0E+00 | 0,0E+00 | |
| 9,7E-04 | 2,5E-01 | 9,5E-01 | 5,5E-05 | 0,0E+00 | 0,0E+00 | |
| 2,1E-05 | 1,4E-01 | 9,4E-01 | 2,8E-06 | 0,0E+00 | 0,0E+00 | |
| 1,7E-07 | 6,7E-02 | 9,3E-01 | 9,2E-08 | 0,0E+00 | 0,0E+00 | |
| 5,3E-10 | 3,1E-02 | 9,2E-01 | 2,1E-09 | 0,0E+00 | 0,0E+00 |
Для вычисления показателей надёжности всей системы необходимо воспользоваться формулами (6), (8) и (9).
Среднее время безотказной работы не зависит от времени и для любого закона распределения вычисляется по формуле Симпсона. При этом шаг h рекомендуется принять равным ti – ti – 1. Число точек n определяется количеством строк таблицы 4, в которых все значения вероятности безотказной работы элементов отличны от нуля. В нашем примере таких строк 4.
На основании полученных в табл. 4-6 массивов необходимо построить графики показателей надёжности (рис. 1-3). Здесь по оси абсцисс откладывается время t в часах, а по си ординат соответственно вероятность безотказной работы, плотность распределения времени безотказной работы или интенсивность отказов.
Таблица 5
Плотность распределения времени безотказной работы элементов и системы
| Время t | Элементы | Система | ||||
| TN(390; 100) | Г(9; 65) | Exp(8·10-5) | R(2·10-5) | W(5; 200) | ||
| 2,0E-06 | 8,00E-05 | 0,0E+00 | 0,0E+00 | 8,2E-05 | ||
| 6,0E-05 | 2,6E-06 | 7,94E-05 | 3,3E-03 | 1,5E-03 | 4,5E-03 | |
| 6,6E-04 | 1,4E-04 | 7,87E-05 | 3,6E-03 | 9,2E-03 | 5,3E-03 | |
| 2,7E-03 | 7,8E-04 | 7,81E-05 | 2,0E-03 | 6,4E-05 | 9,0E-06 | |
| 4,0E-03 | 1,7E-03 | 7,75E-05 | 6,5E-04 | 5,1E-15 | 8,2E-17 | |
| 2,2E-03 | 2,1E-03 | 7,69E-05 | 1,3E-04 | 3,8E-43 | 2,1E-46 | |
| 4,4E-04 | 2,0E-03 | 7,63E-05 | 1,8E-05 | 5,9E-106 | 3,2E-111 | |
| 3,3E-05 | 1,5E-03 | 7,56E-05 | 1,6E-06 | 3,0E-228 | 3,8E-236 | |
| 8,9E-07 | 9,1E-04 | 7,50E-05 | 8,8E-08 | 0,0E+00 | 0,0E+00 | |
| 9,0E-09 | 5,0E-04 | 7,44E-05 | 3,3E-09 | 0,0E+00 | 0,0E+00 | |
| 3,3E-11 | 2,5E-04 | 7,38E-05 | 8,2E-11 | 0,0E+00 | 0,0E+00 |
Таблица 6
Интенсивность отказов элементов и системы
| Время t | Элементы | Система | ||||
| TN(390; 100) | Г(9; 65) | Exp(8·10-5) | R(2·10-5) | W(5; 200) | ||
| 2,0E-06 | 0,0E+00 | 8,0E-05 | 0,0E+00 | 0,0E+00 | 8,2E-05 | |
| 6,0E-05 | 2,6E-06 | 8,0E-05 | 4,0E-03 | 1,6E-03 | 5,7E-03 | |
| 6,8E-04 | 1,4E-04 | 8,0E-05 | 8,0E-03 | 2,5E-02 | 3,4E-02 | |
| 3,3E-03 | 8,2E-04 | 8,0E-05 | 1,2E-02 | 1,3E-01 | 1,4E-01 | |
| 8,6E-03 | 2,0E-03 | 8,0E-05 | 1,6E-02 | 4,0E-01 | 4,3E-01 | |
| 1,6E-02 | 3,4E-03 | 8,0E-05 | 2,0E-02 | - | - | |
| 2,5E-02 | 4,6E-03 | 8,0E-05 | 2,4E-02 | - | - | |
| 3,4E-02 | 5,7E-03 | 8,0E-05 | 2,8E-02 | - | - | |
| 4,3E-02 | 6,7E-03 | 8,0E-05 | 3,2E-02 | - | - | |
| 5,3E-02 | 7,5E-03 | 8,0E-05 | 3,6E-02 | - | - | |
| 6,3E-02 | 8,1E-03 | 8,0E-05 | 4,0E-02 | - | - |
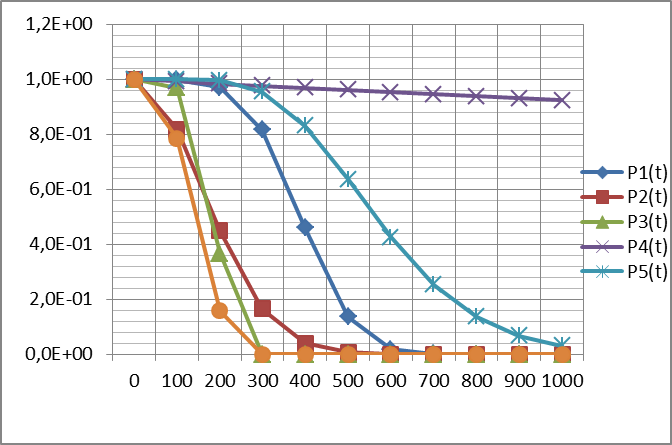
Рис. 1. Зависимость вероятности безотказной работы элементов и системы от времени
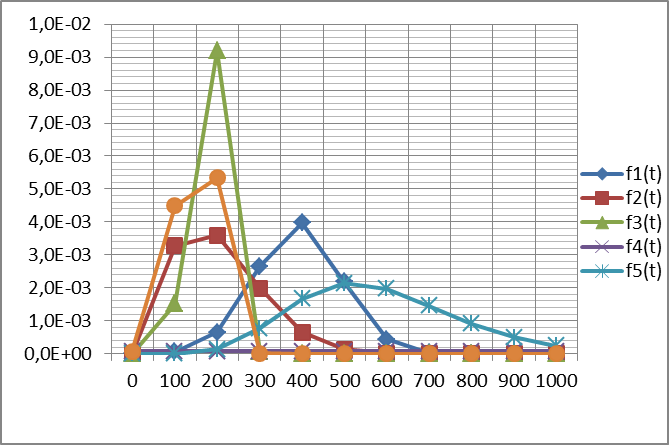
Рис. 2. Зависимость плотности распределения времени безотказной работы элементов и системы от времени
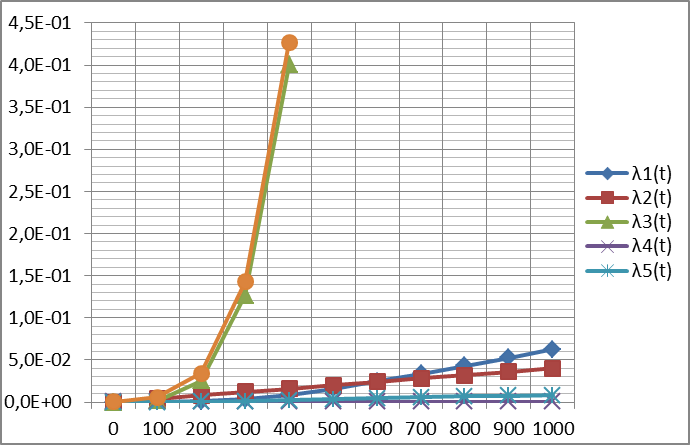
Рис. 3. Зависимость интенсивности отказов элементов и системы от времени
На основании графиков можно сделать вывод о влиянии на надёжность системы каждого из элементов, так, в нашей задаче «слабым звеном» является элемент 5.
| <== предыдущая страница | | | следующая страница ==> |
| ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ | | | ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ |
Дата добавления: 2014-10-17; просмотров: 721; Нарушение авторских прав

Мы поможем в написании ваших работ!