
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Коэффициент усиления объекта
y(  ) 9[ oC ] oC
) 9[ oC ] oC
K = = = 0,18
 x 50[ B ] B
x 50[ B ] B
 x =
x =  U = 50 B
U = 50 B
Далее расчёты производятся на ЭВМ, пакет «TAU», который содержит пять этапов:
Этап 1.
Расчёт коэффициентов дифференциального уравнения методом интегральных площадей (метод Симою)
Исходные данные:
интервал разбиения оси абсцисс кривой разгона 0,75
установившееся значение параметра 0,18
число точек при расчёте кривой разгона 11,0
Вводим значения ординат переходной функции.
Обработка экспериментальной кривой разгона:

Рисунок 1.
Проверка правильности аппроксимации переходной функции.
 x=1
x=1
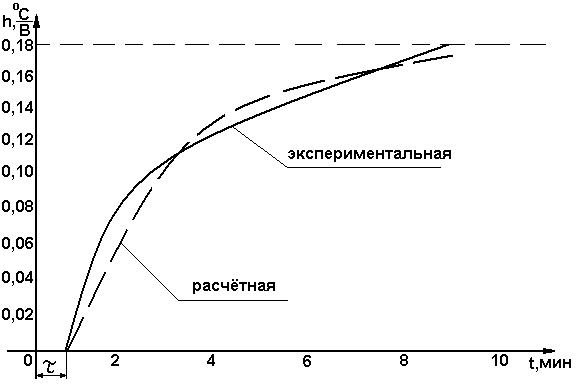
Рисунок 2.
Результаты расчёта :
Коэффициенты дифференциального уравнения объекта:
1-й коэф. = 2,19
2-й коэф. = 0,40
3-й коэф. = 0,00
Динамические характеристики объекта:
дифференциальное уравнение объекта
0,40y’’ (t) + 2,19y’ (t) + y (t) = 0,18x (t – 0,75)
передаточная функция
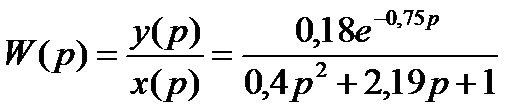
Этап 2.
Проверка точности аппроксимации. ЭВМ находит решение дифференциального уравнения, сравнивает экспериментальную и расчетную переходные функции.
Исходные данные:
длительность переходного процесса 7,5 (мин)
шаг печати результатов 0,75
установившееся значение параметра 0,18
Результаты расчёта :
| Кривая разгона | Расчёт h(t) | Ошибка ( % ) |
| 0,06 | 0,0430 | 28,3290 |
| 0,09 | 0,0855 | 4,9892 |
| 0,11 | 0,1150 | 4,5301 |
| 0,13 | 0,1353 | 4,0507 |
| 0,14 | 0,1492 | 6,5866 |
| 0,15 | 0,1588 | 5,8820 |
| 0,16 | 0,1654 | 3,3934 |
| 0,17 | 0,1700 | 0,0148 |
| 0,174 | 0,1731 | 0,5159 |
Максимальная ошибка 28,3290
По полученным результатам строим расчётную и экспериментальную переходные функции (см. Рисунок 2.).
Запишем выражения для частотных характеристик объекта:
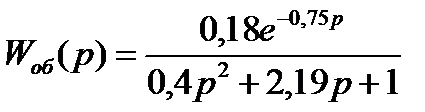 ; заменим р на (-i
; заменим р на (-i 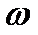 -m
-m 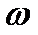 )
)
заменим р на i 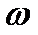 .
.
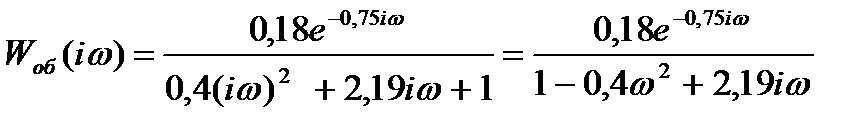
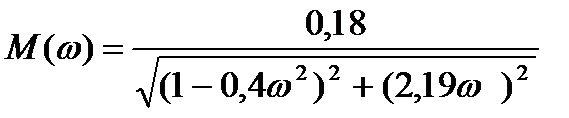
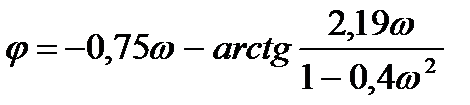
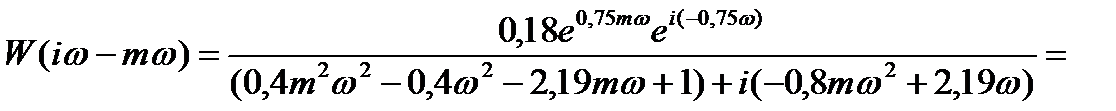
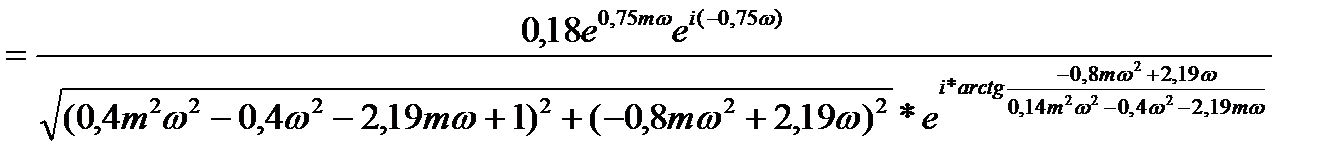
M(m, 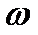 ) =
) = 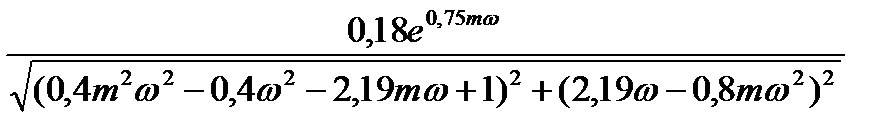

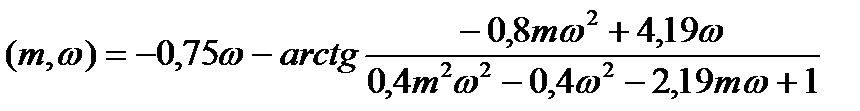
Этап 3.
Расчёт частотных характеристик объекта на ЭВМ.
Расчёт производится 2 раза для m = 0 и m = 0,221 ( расширенная частотная характеристика).
Исходные данные:
степень колебательности 0,00 ; 0,221
нижняя граница частоты 0,00
верхняя граница частоты 2,00
передаточный к-т объекта 0,18
время запаздывания 0,75
1-ой к-т д/у 2,19
2-ой к-т д/у 0,40
3-ой к-т д/у 0,00
Результаты расчёта:
| m = 0 | m = 0,221 | ||||
| частота | РАЧХ(АЧХ) | -(РФЧХ)(ФЧХ) | частота | РАЧХ | -(РФЧХ) |
| 0,67 | 0,11 | 89,0 | 0,59 | 0,13 | 89,0 |
| 0,81 | 0,09 | 0,71 | 0,12 | ||
| 0,95 | 0,08 | 0,84 | 0,10 | ||
| 1,09 | 0,07 | 0,96 | 0,09 | ||
| 1,24 | 0,07 | 1,09 | 0,08 | ||
| 1,38 | 0,06 | 1,21 | 0,07 | ||
| 1,52 | 0,05 | 1,34 | 0,07 | ||
| 1,66 | 0,05 | 1,46 | 0,06 | ||
| 1,80 | 0,05 | 1,59 | 0,06 | ||
| 1,94 | 0,04 | 1,71 | 0,05 |
По полученным данным строим графики (см. рис. 4).
Расчётные данные дополняем известными значениями M( 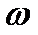 =0) = K;
=0) = K;  (
( 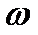 =0) = 0
=0) = 0
Примечание: Вывод уравнений для расширенных частотных характеристик при степени колебательности m=0,221 рассмотрим в лабораторной работе №2.
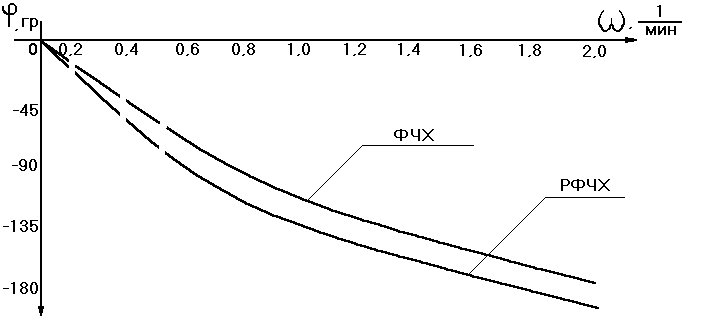
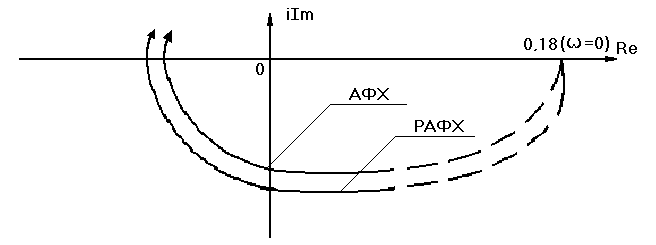
Частотные характеристики объекта:
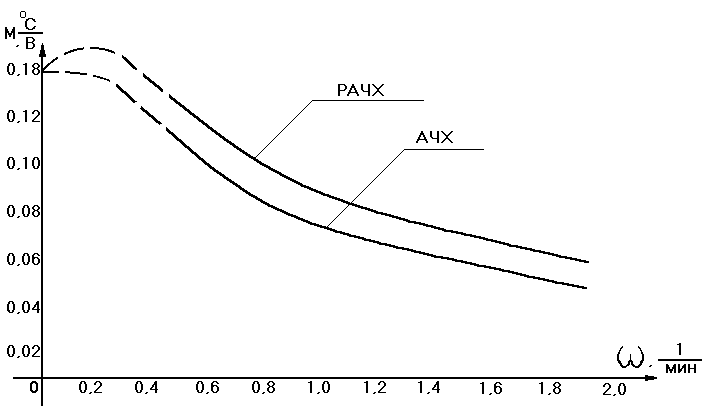
Рисунок 4.
Вопросы к защите лабораторной работы.
1. Что такое объект регулирования. Привести примеры.
2. Методика экспериментального определения статических и динамических характеристик объекта.
3. Что такое кривая разгона и переходная характеристика объекта регулирования.
4. Что такое статическая характеристика объекта. Привести примеры линейных и нелинейных статистических характеристик.
5. Как определить , линеен ли объект регулирования.
6. Как выбрать форму и величину возмущения для получения кривой разгона, как реализовать это возмущение.
7. Какие характеристики объекта могут быть получены по кривой разгона.
8. Что такое коэффициент усиления объекта, как его вычислить.
9. Как определить по кривой разгона коэффициенты диф. уравнения объекта.
10. Если имеется диф. уравнение объекта, как получить его переходную функцию (кривую разгона).
11. Имея диф. уравнение объекта, получить его передаточную функцию, и наоборот.
12. Физический смысл частотных характеристик линейного объекта, пояснить графиками.
13. Построение АФХ объекта по его АЧХ и ФЧХ.
| <== предыдущая страница | | | следующая страница ==> |
| Определение статических и динамических характеристик объекта | | | Лабораторная работа №2 |
Дата добавления: 2014-10-17; просмотров: 1012; Нарушение авторских прав

Мы поможем в написании ваших работ!