Лекция №4

Методология решения проектных задач с помощью средств вычислительной техники.

Лекция №4

Тема: Разбиение задачи проектирования на части

Цель: -на основе анализа методов выбора обобщенных показателя и критерия выявить наиболее часто используемые при проектировании СУ.

Вопросы:

1. Основные частные показатели и критерии задачи принятия решений.

2. Обоснование формирования обобщенного показателя.

3. Методы формирования обобщенного критерия.

4. Особенности расчетов в среде EXCEL.

5. Основные требования ГОСТ.

1. Основные частные показатели и критерии задачи принятия решений.

Выбор показателей оценки эффективности систем и подсистем – сложный процесс, и особенно для сложных систем. Обосновываются показатели с большой осторожностью, после глубокого анализа целей и задач, поставленных перед системой. В общем случае совокупность показателей зависит от:

· структуры системы и характера связей между элементами;

· вида управляющих алгоритмов и закономерностей функционирования;

· параметров внешней среды.

Несмотря на большое количество факторов, влияющих на выбор показателя эффективности, можно выделить ряд закономерностей.

После формулировки целей проектирования обычно приступают к определению одного или нескольких вариантов построения системы, которые заслуживают дальнейшего рассмотрения. Из множества подходов к этому вопросу остановимся на одном из принятых [1]. Всякая сложная система существует в некоторой области значений количественных и качественных показателей эффективности, т.е.

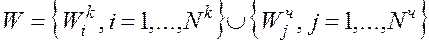, (1)

где W – множество частных показателей эффективности системы;

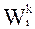- качественные показатели (i – тый);

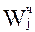- числовые показатели (количественные) (j – тый);

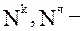мощности множеств.

Качественные показатели, как правило, характеризуют наиболее существенные свойства системы и каждый из них не может быть выражен одним численным значением (к примеру, характеристики дизайна, морального старения и т.д.).

Количественные показатели принимают численные значения и в явном виде характеризуют некоторую сторону функционирования системы, ее структуру, степень выполнения функций и т.д. Показатели характеризуют, как правило, одно или несколько свойств системы или подсистемы. В целях общности с ранее изученным рассмотрим свойства и показатели.

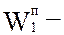помехозащищенность – способность к достоверному приему и переработке информации в системе в условиях помех. Оценивается показателями 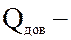вероятность правильного доведения сообщения;

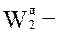достоверность – способность системы к обмену неискаженной информацией в условиях воздействия помех. Оценивается показателями 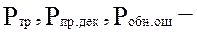соответственно вероятность трансформации, вероятность правильного декодирования, вероятность обнаружения ошибки.

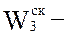скрытность – способность удовлетворять требованиям недопущения определения маршрутов прохождения информации и расшифровки ее содержания, в т.ч. по анализу ЭМИ. Может оцениваться 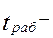временем работы радиосредства при доведении сообщения заданной длины.

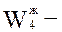живучесть – способность системы выполнять заданные функции при отказах отдельных узлов и физических каналов СПД. Будем оценивать величиной, равной 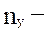максимальному количеству отказавших узлов, при которых система еще работоспособна.

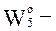оперативность – способность реагировать и исполнять команды, распоряжения, запросы должностных лиц в заданных временных ограничениях при требуемом уровне достоверности информации. Будем оценивать 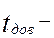временем доведения информации.

Таким образом, каждый вариант может характеризоваться совокупностью частных показателей:

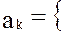
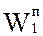
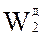
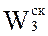
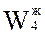
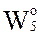
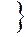, оцениваемых кортежем

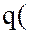
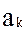
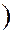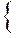
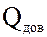
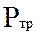
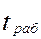
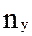
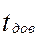
= , элементы которого учитываются при решении задачи выбора (принятия проектного решения).

Пример:

а₁ : {0,99 0,0001 0,5 5 1,1}

2. Обоснование формирования обобщенного показателя

В качестве примера рассмотрим возможность решения задачи выбора из множества альтернатив, мощность которого равна 3. Т.е. К=3, А={a₁ a₂ a₃}. Для каждого варианта известны показатели и критерии:

а₁ : {0,99 0,0001 0,5 5 1,1}

а₂ : {0,99 0,0001 0,5 10 1,1}

а₃ : {0,993 0,00015 0,6 9 1,2}

Выбор из первых двух очень прост. Второй явно предпочтительней, поскольку четвертый показатель наилучший, а все остальные - одинаковые. Трудности возникают при выборе между вторым и третьем вариантом. Не имея формального правила, выбор сделать невозможно, и тем более автоматизированно. Существует несколько методов формирования обобщенного критерия.

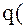
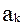
Рассмотрим возможные методы формирования обобщенного критерия Е, если известны частные показатели (кортеж 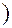). В этом случае решается задача выбора и выглядит это решение следующим образом.

Имеется некоторое множество А вариантов построения системы, причем каждый вариант 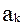, , 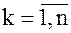характеризуется определенной совокупностью свойств, каждое из которых оценивается частным показателем 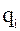, , 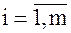т.е. имеется кортеж показателей 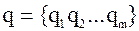, количественно отражающих множество свойств системы. Тогда К-тый вариант построения системы может однозначно характеризоваться вектором 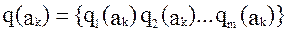, и требуется принять решение о выборе одного из вариантов. Как правило, в САПР этот выбор должен состояться по формальному признаку, сводящемуся к отысканию отображения 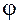, которое каждому вектору q ставит в соответствие действительное число 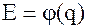, определяющее степень предпочтительности данного решения. Оператор 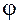и называют обобщенным критерием эффективности системы. Рассмотрим основные методы формирования обобщенного критерия.

Существует много методов формирования обобщенного показателя и критерия. Рассмотрим основные, наиболее часто встречающиеся.

3 Методы формирования обобщенного критерия

1. Маргинальный метод наиболее простой. За обобщенный принимается один из частных, все остальные учитываются в виде ограничений, определяющих область допустимых значений, т.е.

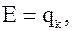
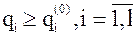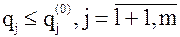, , где 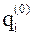- допустимые значения показателей. Со знаком берутся те показатели, которые желательно увеличить, со знаком 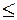- уменьшить. Полученные результаты будут существенно зависеть от корректности выбора ограничений.

22. Метод простых (аддитивных и мультипликативных) преобразований над выбранной системой частных показателей. Для случая аддитивных

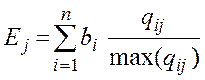, (2)

где 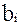- весовые коэффициенты, положительные – для тех, которые желательно максимизировать, а отрицательные – минимизировать. Недостаток – возможность компенсации за счет различных показателей. Для устранения этого недостатка вводят ограничения на значения показателей .

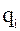3. Метод оценки по расстоянию до идеального значения. Чем ближе показатели рассматриваемой системы к идеальной, тем она предпочтительнее. В качестве идеальной обычно принимаются значения 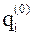, достижимые на современном уровне развития техники или в перспективе. Для показателей одной размерности суммы абсолютных отклонений

,

где под первым знаком суммы показатели, подлежащие максимизации, под вторым – минимизации.

Для показателей разной размерности – суммы относительных отклонений

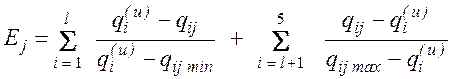(3)

Существуют и другие методы формирования обобщенного критерия.

4. Особенности расчетов в среде EXCEL

Определить наилучший вариант по обобщенному показателю, сформированному на основе метода простых преобразований, весовые коэффициенты взять одинаковыми по абсолютной величине.

Решение:

1. Запишем формулу для расчета обобщенного показателя (вызвать к доске курсанта и предложить записать и пояснить данную формулу):

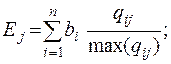
2. Находим весовые коэффициенты b_i. Поскольку в задании определено, что они одинаковы по абсолютной величине, то b_i =1/5=0,2. Второй, третий и пятый показатели желательно минимизировать, следовательно, они должны быть отрицательными (b₂=b₃=b₅= - 0,2).

3. Находим максимальные значения частных показателей:

q₁ : max q_1j = q₁₃ = 0,993;

q₂ : max q_2j = q₂₃ = 0,00015;

q₃ : max q_3j = q₃₃ = 0,6;

q₄ : max q_4j = q₄₂ = 10;

q₅ : max q_5j = q₅₃ = 1,2;

4. Подставляем значения в формулу и производим вычисления. Обратить внимание на правильную подстановку - числовые значения должны следовать в том же порядке, что и параметры в формуле.

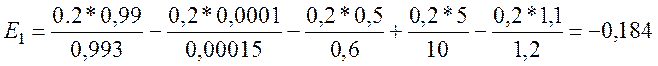
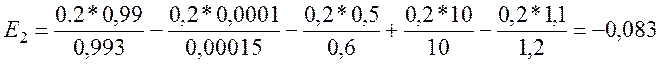
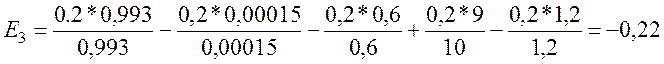
Определить наилучший вариант по обобщенному показателю, сформированному на основе определения минимального расстояния до идеального значения, заданного вектором :

.

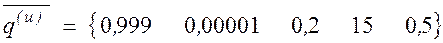Решение:

Запишем формулу для расчета относительного расстояния (вызвать к доске курсанта и предложить записать и пояснить данную формулу):

,

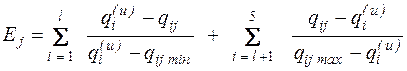Максимизировать нужно Q_дов (q₁) и n_у (q₄), минимизировать – остальные. Первая часть формулы для параметров максимизируемых, вторая - для минимизируемых. Для формального использования зависимости требуется перенумерация показателей. Для рассматриваемого варианта l=2.

Найдем из представленных альтернатив максимальные и минимальные значения для:

q₁: min q_1j = q₁₁ = q₁₂ = 0,99;

q₂: max q_2j = q₂₃ = 0,00015;

q₃: max q_3j = q₃₃ = 0,6;

q₄: min q_4j = q₄₁ = q₄₂ = 5;

q₅: max q_5j = q₅₁ = q₅₂ = 5;

Обратить внимание, что при данном методе должны быть определены (в отличие от предыдущего) в одном случае минимальные, в другом-максимальные значения частных показателей.

Подставим значения в формулу:

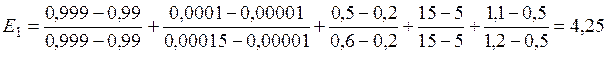
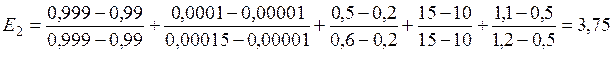
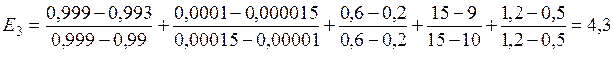
Записать проектное решение для данных вариантов построения системы.

Дата добавления: 2014-10-17; просмотров: 403; Нарушение авторских прав

Мы поможем в написании ваших работ!