Задачи классической механики

Число частиц во Вселенной огромно, все они взаимодействуют друг с другом. Радиус электромагнитного и гравитационного взаимодействий не ограничен. Поэтому решить задачу о движении какой-либо частицы, учитывая все взаимодействия, не представляется возможным даже в рамках классической механики. При решении любой задачи мы можем делать последовательные упрощения, пренебрегая некоторыми взаимодействиями. Самая сложная модель, которую мы построим, решая задачу, будет учитывать максимальное число взаимодействий. Самая простая модель будет учитывать немногие самые сильные взаимодействия между телами.

Далее решим ряд задач, в которых будем анализировать модели с разной степенью упрощения. Например, решая задачу о финитном движении тела в области минимума потенциальной энергии, начнем с простейшей модели, в которой учитывается только одно взаимодействие. В результате получим уравнение гармонического осциллятора, решением которого будет гармоническая функция. Затем учтем взаимодействие колеблющегося тела со средой, решением этой задачи будет гармоническая функция модулированная по амплитуде. Следующая по сложности модель будет учитывать еще одно внешнее периодическое воздействие.

Естественно, по мере усложнения модели, трудности решения уравнений движения будут нарастать. Дилемма проста: чем проще модель, тем менее точное решение получаем, для слишком сложной модели можем не справиться с математическими трудностями. Особое отношение в физике у нас к тем моделям, для которых еще можно получить решение в виде аналитической функции. Такое решение очень удобно для анализа. Большинство результатов в физике представлены именно в такой форме.

В последнее время благодаря развитию компьютеров многие задачи мы решаем численно. В этом случае решение будет менее наглядным, хотя, варьируя различные параметры задачи и строя графики зависимости искомой величины от того или иного параметра, можно полностью проанализировать решение.

Движение твердого тела

Самые общие законы механики, которые мы сформулировали применительно к материальным точкам, можно использовать и для описания движения тел, имеющих конечные размеры. В этом случае мы разбиваем его на малые части, которые можно считать материальными точками. В теле конечных размеров между его малыми элементами есть взаимодействие, которое может сложным образом меняться после приложения к телу внешних сил. Для упрощения задачи далее в этом разделе будем рассматривать абсолютно твердые тела, деформациями которых можно пренебречь.

§13 Уравнения движения твердого тела

Итак, задача о движении тела конечных размеров сводится к задаче о движении системы из материальных точек, разбиением тела на малые элементы с массами 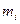, которые можно считать материальными точками (рис.13.1). В абсолютно твердом теле расстояние от каждого малого элемента тела до его центра инерции R_i - величина постоянная.

Рис.13.1

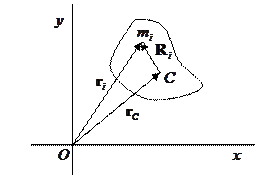
Учитывая это, мы можем описать движение твердого тела в виде суперпозиции двух движений:

1) движения материальной точки с массой, равной массе тела М, и скоростью, равной скорости центра масс ;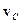

2) вращения твердого тела вокруг оси, проходящей через центр масс, с угловой скоростью .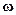

Уравнение, описывающее движение центра масс получим, используя выражение для импульса тела :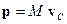

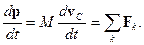(13.1)

Центр инерции твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием приложенных к нему сил. Поскольку тело имеет конечные размеры и не все силы приложены к центру масс, суммарный момент приложенных сил относительно центра масс может быть не равен нулю. Однако для описания движения центра масс это неважно. Отличие от нуля суммарного момента сил, действующих на тело, приводит к тому, что тело вращается вокруг оси, проходящей через центр масс с меняющейся во времени угловой скоростью.

Момент импульса тела также будет меняться под действием суммарного момента сил:

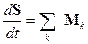. (13.2)

Кинетическая энергия движущегося твердого тела будет складываться из кинетической энергии поступательного и вращательного движений. Если деформациями тела пренебречь нельзя, то к этим двум слагаемым в общей энергии движущегося тела добавиться потенциальная энергия упругой деформации и внутренняя энергия, которая будет увеличиваться при неупругой деформации.

§14 Осевой момент инерции твердого тела

Рассмотрим вращение твердого тела вокруг неподвижной оси 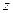(рис.14.1), проходящей через начало координат 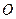. Момент импульса части тела массы 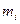, положение которой задается радиус-вектором 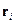(эта часть находится в плоскости рисунка, ее вектор скорости перпендикулярен плоскости рисунка, в которой лежат все остальные вектора), будет равен:

,

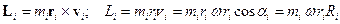где 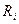- кратчайшее расстояние массы 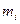до оси вращения. Проекция этого вектора на ось 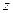будет равна:

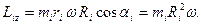
Для проекции момента импульса тела на ось 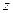получим:

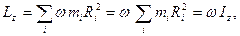
где 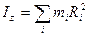- момент инерции твердого тела относительно оси .

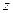Переходя от суммирования к интегрированию после предельного перехода, для осевого момента инерции получим выражение:

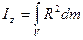, (14.1)

где интегрирование ведется по всему объему тела V.

Рис.14.1

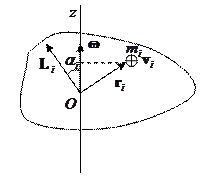
Момент инерции относительно различных осей вращения будет различен. Найдем связь момента инерции относительно оси, проходящей через центр масс 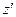, и любой другой оси 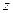, параллельной ей, отстоящей от нее на кратчайшее расстояние а (рис.14.2).

В этом случае связь моментов инерции, определенных относительно этих осей, называют теоремой Штейнера. Воспользовавшись результатом из §12, получим:

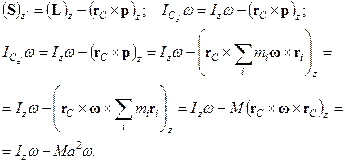
Рис.14.2

Итак, получили уравнение, связывающее моменты инерции:

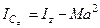(14.2)

Кроме этого соотношения можно отметить другое полезное соотношение, связывающее моменты инерции относительно трех взаимно перпендикулярных осей 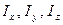. Сначала отметим, что

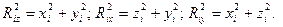
Умножив на массы и просуммировав, получим:

,

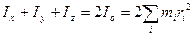где 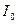некоторая вспомогательная величина, не имеющая физического содержания, но использование которой, полезно при вычислениях осевых моментов инерции различных тел:

.

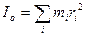Определим моменты инерции некоторых симметричных однородных тел относительно трех взаимно перпендикулярных осей, проходящих через центр масс.

1. Шар массы m, радиуса R. Все осевые моменты инерции равны. Тогда для I_z получим:

.

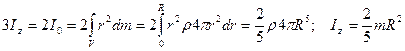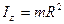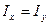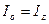2. Обруч массы m, радиуса R. Ось z – ось симметрии, перпендикулярная плоскости, в которой лежит обруч. Тогда , и, поскольку , а , для осевого момента инерции 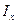получим значение:

.

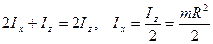3. Тонкий диск массы m радиуса R. Если ось z перпендикулярна плоскости диска, то

,

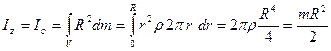где 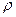- масса диска, отнесенная к его площади. Другие осевые моменты инерции равны:

.

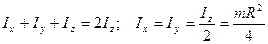4. Тонкий стержень массы m длины L. Для оси, совпадающей со стержнем момент инерции равен нулю, для двух других осевых моментов инерции получим значения:

,

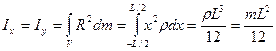где 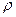- масса единицы длины стержня.

Дата добавления: 2014-11-01; просмотров: 401; Нарушение авторских прав

Мы поможем в написании ваших работ!