Частотные характеристики параллельного контура

Построим резонансную кривую тока в неразветвленной части параллельного контура при постоянном напряжении источника питания для идеального случая 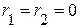(рис. 3.83)

На рисунке 3.84, показаны частотные характеристики проводимости ветве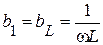й и 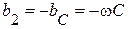и входной проводимости цепи 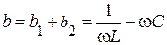. Ток 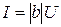, поэтому кривая 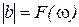в соответствующем масштабе и есть резонансная кривая .

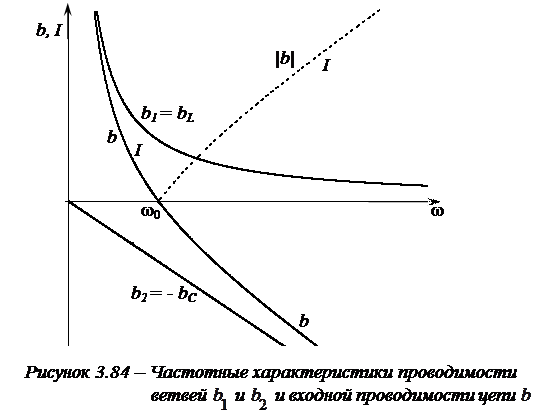При изменении частоты от 0 до 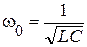эквивалентная проводимость 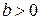, т.е. индуктивная, и изменяется от 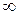до 0. При 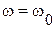наступает резонанс токов, , , 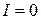и 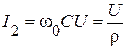. При возрастании частоты от до 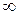входная проводимость , т.е. емкостная, и изменяется от 0 до .

В общем случае при сопротивлениях 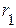и 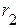, не равных нулю (рис. *.*), входящая активная проводимость цепи отлична от нуля при любой частоте, поэтому ток 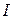ни при одном значении частоты не равен нулю. При услови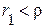и и 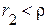зависимость при 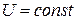имеем минимум, причем этот минимум наблюдается при частоте, отличающейся от резонансной частоты. Максимум полного входного сопротивления получается при частоте, при которой , а резонанс имеет место при частоте, для которой или 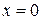. Чем меньше 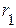и 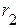, тем меньше минимальное значение тока 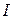, тем ближе значение часты, при которой наблюдается минимум тока, к резонансной частоте и тем больше график похож на кривую при 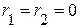(рис. *.*).

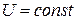При условии и ток 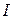при любой частоте одинаков. Зависимость не имеет ни максимума, ни минимума и графически представляется прямой, параллельной оси абсцисс.

Анализ показывает, что при услови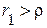и и кривая при некотором значении частоты достигает максимума.

Дата добавления: 2014-02-27; просмотров: 376; Нарушение авторских прав

Мы поможем в написании ваших работ!