
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Подстановка термов в формулы
Формальной подстановкой (или просто подстановкой) называется функция J, определенная на конечном множестве переменных, перерабатывающая каждую переменную х из области определения J в некоторый терм формальную подстановку можно изображать в виде двумерной таблицы
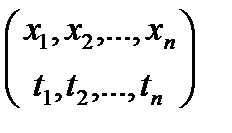 ,
,
где в верхней строке указана область определения функции J:
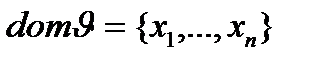 , и
, и
J(xi)=ti.
Пусть Т –формула или терм логики предикатов и J-формальная подстановка 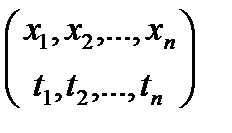 . Через ТJ=Т
. Через ТJ=Т 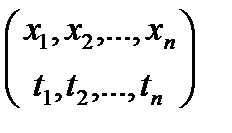 =
= 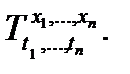
Другое обозначение подстановки-множество q={x1/t1, x2/t2,…,xn/tn}, где xi и ti, iÎ 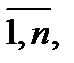 являются соответственно переменными и термами.
являются соответственно переменными и термами.
Выражение (атом, терм, формула) Тq обозначает выражение, полученное путем подстановки на места свободных вхождений переменных x1,…, xn соответствующих термов t1,…, tn.
Если вместо переменных в выражение ничего не подставляется, то подстановка называется пустой. Пустая подстановка обозначается символом Е, E={ }.
Дадим индуктивное определение подстановки.
1. 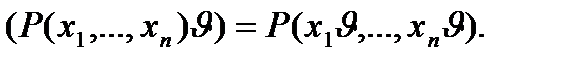
2. 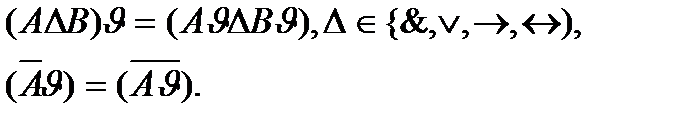
Не все подстановки одинаково пригодны с точки зрения логики. При выполнении подстановки терма в формулу, важно учитывать следующее:
Вместо связанных переменных ничего подставлять нельзя.
Нельзя допускать появления новых связанных вхождений какой-нибудь переменной, если их не было в исходной формуле.
Результат подстановки термов t1 t2 ... tn в формулу Р вместо свободно входящих переменных х1, х2, ..., хn обозначается 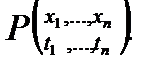 или P{x1/t1,…xn/tn}, где {x1/t1,…, xn/tn} называется подстановкой.
или P{x1/t1,…xn/tn}, где {x1/t1,…, xn/tn} называется подстановкой.
Определение: переменная у свободна для переменной х в формуле Р, если в формуле Р отсутствуют свободные вхождения переменной х, находящиеся в области действия квантора по переменной у; терм t свободен для переменной х в формуле Р, если любая переменная терма свободна для х в формуле Р.
Следствия.
Постоянный терм свободен для любой переменной в любой формуле Р.
Если ни одна переменная терма не является связанной переменной формулы Р, то терм t свободен для любой переменной формулы Р.
Практически это означает, что свободный для переменной х терм может быть подставлен в формулу Р вместо свободного вхождения переменной х, не изменив ее логического значения. Например, формула (x+y<0) содержит переменные х и у свободно. Логическое значение замыкания этой формулы получается навешиванием квантора общности по свободным переменным, в модели M=(R,<), где R-множество действительных чисел, I["х"у(x+y<0)]=0. Пусть терм t=y2-y. Согласно определению терм t свободен для переменной х в этой формуле. Результатом подстановки будет формула (у2-у+у<0), логическое значение которой I["y(y2 <0)]=0,и совпадает со значением формулы до подстановки.
Связав переменную у квантором существования, получим формулу $у(х+у<0). Логическое значение замыкания этой формулы I["x$y(x+y<0)]=1, т.е. высказывание: Для любого действительного числа х существует действительное число у, для которого х+у<0 - истинно на множестве действительных чисел R. Переменная у не свободна для переменной х в последней формуле. Результатом подстановки в формулу терма t вместо свободно входящей переменной x: 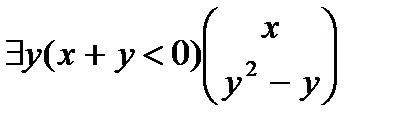 , является предложение
, является предложение 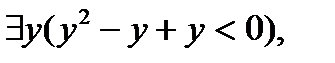 которое ложно в множестве действительных чисел R. В результате подстановки терма t в формулу вместо свободного вхождения переменной x произошла смена логического значения формулы. Такое событие называется коллизией переменных.
которое ложно в множестве действительных чисел R. В результате подстановки терма t в формулу вместо свободного вхождения переменной x произошла смена логического значения формулы. Такое событие называется коллизией переменных.
Далее будут приведены общезначимые равносильности логики предикатов, среди которых имеется равносильность, утверждающая возможность переименования связанных переменных. Чтобы избежать коллизии переменных, необходимо перед подстановкой терма в формулу произвести переименование всех связанных переменных формулы, встречающихся в терме. Действительно, результатом переименования связанной переменной у на переменную u, является формула 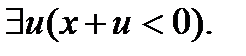 Подставив в нее тот же терм, получим истинную формулу.
Подставив в нее тот же терм, получим истинную формулу.
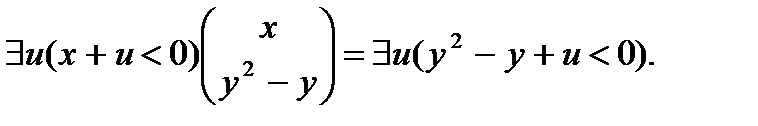
| <== предыдущая страница | | | следующая страница ==> |
| Метод семантических таблиц | | | Исчисление предикатов |
Дата добавления: 2014-11-08; просмотров: 633; Нарушение авторских прав

Мы поможем в написании ваших работ!