Метод резолюций

В математической логике и автоматическом доказательстве теорем правило резолюций восходит к методу доказательства теорем через поиск противоречий. Правило резолюций применяется последовательно для списка резольвент и позволяет ответить на вопрос, существует ли в исходном множестве логических выражений противоречие. Правило разработано Джоном Аланом Робинсоном в 1965.

Алгоритмы доказательства выводимости: 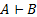, построенные на основании этого метода, применяются в системах искусственного интеллекта, а также являются фундаментом, на котором построен язык логического программирования ПРОЛОГ.

Пусть 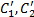– два предложения в исчислении высказываний, и пусть 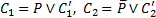, где Р – пропозициональная переменная, а 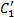и 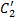– любые предложения (в частности, возможно, пустые или состоящие из одного литерала).

Правило вывода

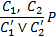
называется правилом резолюции.

Предложения 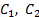называются резольвируемыми (родительскими), предложение 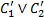– резольвентой, а атомные формулы 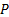и 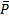– контрарными литералами. В правиле резолюции из двух исходных выражений получается новое выражение, содержащее все литералы двух исходных предложений, за исключением двух взаимно обратных литералов.

Доказательство теорем сводится к доказательство того, что некоторая формула G (гипотеза теоремы) является логическим следствием множества формул 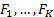(допущений).Сама теорема может быть сформулирована следующим образом: «Если 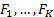истинны, то истинна также формула G.

Для доказательства вначале составляется множество формул 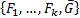. Затем каждая из этих формул приводится к КНФ. Каждой кратной дизъюнкции в КНФ сопоставляется множество, содержащее все входящие в нее атомы с теми значениями истинности, которые они имеют в дизъюнкте. Такие множества также называются дизъюнктами. Также в КНФ знаки конъюнкции заменяются запятыми. Результатом является множество дизъюнктов S, представленное в теоретико-множественной форме.

Формула G является логическим следствием множества дизъюнктов S, если из нее выводим пустой дизъюнкт, который обозначается символом ÿ (из библиотеки “symbol”). Если из S нельзя вывести пустой дизъюнкт ÿ, то G не является логическим следствием формул 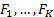. Такой метод доказательства теорем называется методом резолюций.

Пример:

Пусть имеются следующие утверждения (исходное знание):

1. Яблоко красное и ароматное.

2. Если яблоко красное, то яблоко вкусное.

Выделим здесь три атома:

R – яблоко красное (red)

A – яблоко ароматное (aroma)

D – яблоко вкусное (delicious).

Теперь исходные утверждения можно представить в виде формул:

F1: R & A,

F2: .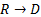

Формулировка задачи имеет вид:

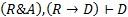
В теоретико-множественном представлении это можно записать как

Построение доказательства рекомендуется начинать с последнего дизъюнкта – цели. В нашем случае он резольвирует с третьим дизъюнктом, порождая новый дизъюнкт 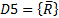. Этот новый дизъюнкт резольвирует с первым дизъюнктом 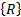, порождая пустой дизъюнкт.

Получение пустого дизъюнкта означает, что множество S противоречивое, и оно стало таким в результате введения отрицания цели. Следовательно сложное исходное высказывание доказано.

Дата добавления: 2014-11-08; просмотров: 501; Нарушение авторских прав

Мы поможем в написании ваших работ!