Исчисление секвенций в PL

Исчисление секвенций (ИС) – это формальная система, в которой в алфавит языка логики высказываний добавлен символ следования, обозначаемый ├, который читается «выводимо» или «доказуемо». Правила вывода a├ b (b выводима из a) применяются непосредственно к формулам, а не к таблицам истинности, позволяя из истинности одних формул делать вывод об истинности других формул. Символы a, b в правиле вывода обозначают одну или несколько формул; a называется условием, а b - следствием. Если в условии или следствии формул несколько, то они записываются через запятую. Представляют интерес только такие правила вывода, с помощью которых на основании истинности всех формул, входящих в условие правила вывода, можно при любой интерпретации сделать заключение об истинности всех формул, входящих в следствие правила вывода. Обычно такие правила называют состоятельными.

Понятие формулы в исчислении секвенций определяется, как было определено выше.

Если 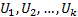, C - формулы, то выражения вида 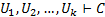называются секвенциями. Далее будем рассматривать секвенции вида:

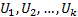
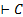· , где k>0, – читается: «из 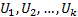следует C»,

· ├ C, – читается: «C доказуема»,

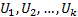
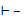· читается: «система 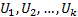- противоречива».

Такие секвенции называются также хорновскими дизъюнктами.

Вывод в ИС - это конечная последовательность секвенций 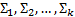такая, что для каждого i, 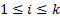, секвенция 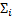есть либо аксиома, либо непосредственное следствие из предыдущих секвенций по правилам вывода.

Секвенция 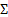называется выводимой в ИС, если существует вывод в ИС, оканчивающийся S. Обозначается следующим образом:

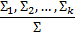
Соответствующее этому выводу правило называется допустимым. Опишем механизм, порождающий все тавтологии.

Для большей наглядности формулировок рассмотрим кроме формул также последовательности формул и секвенции вида Г 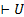, где Г-последовательность формул, возможно пустая, U-формула. Высказывание входит в секвенцию, если оно входит в левую или правую часть секвенции.

Истинность секвенции: секвенция истинна, если при любых логических значениях всех входящих в нее высказываний из истинности всех формул, входящих в левую часть секвенции, следует истинность формулы в правой части секвенции. Секвенция с пустой левой частью истинна, если правая часть тождественно истинна. Остальные секвенции назовем ложными. Истинность секвенции 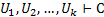равносильна тому, что формула 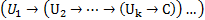является тавтологией.

Самое сильное правило вывода имеет вид: 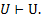Эта секвенция называется схемой аксиом исчисления секвенций. Аксиомой называется выражение, получающееся из схемы аксиом подстановкой вместо атома U конкретной формулы.

Пусть символы Г1, Г2, Г3, Г – означают конечные последовательности формул, возможно пустые, U, A, B, C –произвольные формулы. Основные правила вывода в исчислении секвенций:

В исчислении секвенций используется единственная аксиома, представленная схемой аксиом, и множество правил вывода.

Схема аксиом: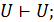

Правила вывода:

1. (Введение конъюнкции):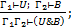

2. (Уд. конъюнкции): ;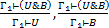

3. (Вв. дизъюнкции):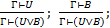

4. (Уд. дизъюнкции): ;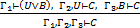

5. (Вв. импликации):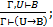

6. (Уд. импликации):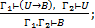

7. (Вв. отрицания):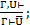

8. (Уд. отрицания):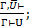

9. (Сведение к противоречию):

10. (Утончение):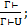

11. (Расширение):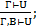

12. (Перестановка): ;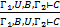

13. (Сокращение): .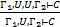

Существует два способа доказательства допустимости правила:

1. В соответствии с определением вывода в исчислении секвенций вывод может начинаться только с аксиом. К ним затем применяются правила вывода, в результате чего получаются новые истинные секвенции. Процесс построения вывода продолжается до тех пор, пока не будет получена заданная секвенция. Такой способ доказательства выводимости секвенций называется прямым выводом.

2. Существенно эффективнее применение обратного вывода, когда вывод строится в виде дерева вывода, в корень которого помещают доказываемую секвенцию. Доказательство строится сверху вниз. Построение дерева продолжается до тех пор, пока листьями в конце каждой ветви дерева будут только аксиомы. Для разделения вершин дерева текущая секвенция отделяется от порождающих ее секвенций горизонтальной линией, против которой указывается примененное на данном шаге правило вывода из числа приведенных выше или полученных дополнительно.

Аппарат исчисление секвенций может использоваться для создания компьютерных программ автоматического доказательства теорем, учитывая, что каждая новая секвенция, полученная в результате вывода, является теоремой.

При использовании прямого вывода для автоматизированного доказательства теорем исчисления высказываний требуется выполнения большого числа переборов, включая выбор подходящих аксиом, и подходящих правил вывода на каждом последующем шаге. При построении доказательства «вручную» в выборе последовательности правил вывода участвует интуиция, которая отсутствует у программы.

В случае прямого вывода к множеству начинающих вывод аксиом может применяться большое число разных правил, и большая часть последовательных шагов алгоритма не приводит к желаемому результату.

В случае обратного вывода поиск нужных правил вывода на каждом шаге алгоритма ограничен структурой порожденных ими секвенций. Поэтому число переборов правил при решении меньше, чем в предыдущем случае.

Рассмотрим пример применения прямого и обратного вывода к доказательству допустимости (истинности) секвенции. Пусть требуется доказать, что секвенция

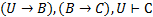
допустима.

Прямой вывод:

1. – аксиома;

2. 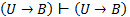– аксиома;

3. 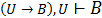; – из (1), (2) и правила 6;

4. 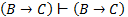– аксиома;

5. – аксиома;

6. 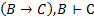– из (4), (5) и правила 6;

7. 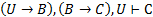– из (3), (4) и правила 12;

При целенаправленном выборе аксиом и правил вывода для решения задачи потребовалось семь шагов.

Обратный вывод:

Для реализации компьютерных программ, выполняющих доказательства теорем в исчислении секвенций, более предпочтительным является обратное доказательство, которое состоит в последовательном подборе аксиом и правил вывода, следствием которых является рассматриваемая секвенция. В этом случае подбор правил вывода является целенаправленным и может быть выполнен меньшим числом переборов. Обратный вывод состоит в построении дерева формул.

Дерево формул есть по определению двумерная фигура, составленная из формул языка по следующим индуктивным правилам:

· каждая формула А является сама по себе деревом формул, нижней формулой этого дерева считается по определению сама формула А.

· если D₁ и D₂ суть деревья с нижними формулами вида А и А®В соответственно, то фигура

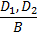
есть дерево формул. Мы говорим, что формула В получена в этом дереве из А и А®В по правилу MP.

Последовательность вхождений формул в дерево, начинающаяся с нижней формулы дерева и продолжающаяся без пропусков до одной из самых верхних формул дерева называется ветвью дерева формул. Количество формул в самой длинной ветви дерева называется высотой дерева формул. Верхние формулы дерева формул, не имеющие вида аксиом исчисления секвенций, называются гипотезами, или открытыми посылками дерева формул.

Применим к рассмотренной секвенции правило обратного вывода:

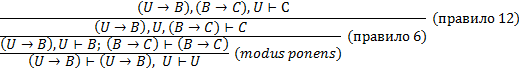
Во втором случае для доказательства потребовалось три шага (три правила).

Дата добавления: 2014-11-08; просмотров: 1234; Нарушение авторских прав

Мы поможем в написании ваших работ!