Анизотропия поверхностного натяжения

Поверхностное натяжение плоской поверхности твердого тела зависитот кристаллографической ориентации образца. В качестве примера рассмотрим двумерное твердое тело, в котором есть одно направление, и поверхность несколько отклонена от него.

В результате поверхность представляет собой плоские террасы длиной в несколько атомом, и ступеньки длиной в атом. θ ~ tgθ = 1/n.

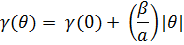
Рассмотрим зависимость производной. Она в точке нуля имеет разрыв. Такую ситуацию называет наличием точки возврата, т.е. минимум, но с неопределенной производной.

В случае больших углов необходимо учитывать возросшую плотность ступенек и…

В работах Ландау показывается, что в этом случае функция зависимости поверхностного натяжения от угла имеет точку возврата при каждом значении угла, который соответствует рациональному значению индекса Миллера. Перепад значений производной быстро уменьшается при росте индекса (пропорционально четвертой степени индекса Миллера).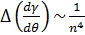

Качественно, мы получим некоторую картину.

Эта зависимость определяет равновесную форму кристалла.

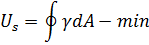
Вульфом было предложено геометрическое решение такой задачи. Для построения формы кристалла берут такую кривую зависимости поверхностного натяжения от угла, в точках возврата строят перпендикуляры к радиус-вектору, и далее утверждается, что внутренняя огибающая это семейство перпендикуляров, и имеет такую форму, какую имеет равновесный кристалл. Показывает ориентацию поверхности в ближайшей точке возврата.

Дата добавления: 2014-11-14; просмотров: 222; Нарушение авторских прав

Мы поможем в написании ваших работ!