Далее будем вводить уравнение Гиббса-Гюгема

Полный дифференциал от энергии:

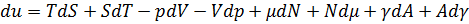
Вычитая одно из другого, получаем следующее:

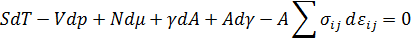
γdA – очевидно, что dA должно быть связано с величиной растяжения, потому что и то и другое отличает за линейные размеры.

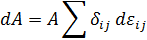
Итого, подставляя уравнение Гиббса-Гюгема, получаем

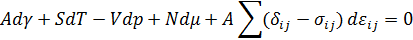
Полученное уравнение называется уравнением адсорбции Гиббса, и является фундаментальным уравнением термодинамики.

Преобразуем данное уравнение таким образом, чтобы оно содержало только величины, связанные с поверхностью. Для этого мы должны прибегнуть к равенствам ранее, и расписать экстенсивные величины как сумму величин трёх областей.

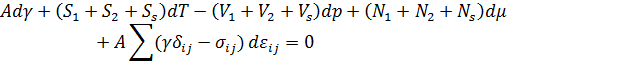
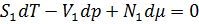
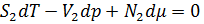
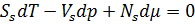
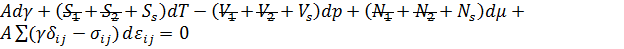-остаются только связанные с поверхностью величины.

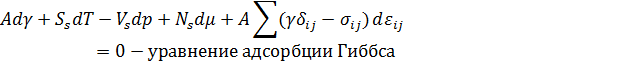
В данном уравнении Гиббса присутствует, как может показаться, 5 независимых переменных: давление, температура, γ, μ, и тензор растяжения ε_ij. На самом деле, поскольку у нас есть еще два уравнения Гиббса для объемных фаз, мы можем сократить количество переменных до трёх, сделав важное упрощение. Исходное уравнение позволяет связать dp, dT и dμ. Для удобства выразим через dT.

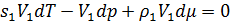
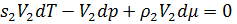
На объем можно сократить. Получаем:

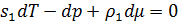
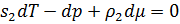
Относительно dp и dμ это линейное уравнение. Получаем:

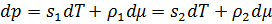
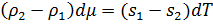
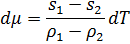𝑑𝑝=𝑠1𝑑𝑇+𝜌1𝑠1−𝑠2𝜌2−𝜌1𝑑𝑇=𝑠2𝑝−𝑠1𝜌1+𝑠1𝜌1−𝑠2𝜌2𝜌2−𝜌1=𝑠1𝜌2−𝑠2𝜌2𝜌2−𝜌1𝑑𝑇

В итоге получаем следующее

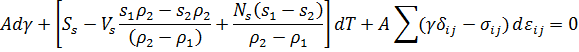
Для анализа стоит заметить важную особенность: то, что стоит в фигурных скобках, не зависит от положения границы раздела, т.е. нигде нет зависимости от V₁ и V₂, поэтому можно выбирать границу раздела, которая нам удобна. Удобно выбрать бесконечно тонкую границу раздела, это значит, что объем V_s можно положить равным 0, и как следствие из этого, число частиц из этого предполагаем как нулевое. Несмотря на это, сам факт наличия границы между двумя фазами предполагает наличие избытков энергии, и все члены остаются. Исходя из этого, можно сократить уравнение Гиббса до следующего вида:

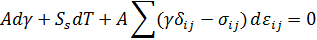
Из уравнения в такой форме можно сделать несколько важных выводов о состоянии поверхности:

1. В состоянии покоя (не происходит никакого растяжения), энтропия поверхности .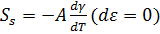

2. С другой стороны, при постоянной температуре мы должны рассматривать последнее слагаемое для каждой величины отдельно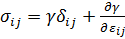

Здесь нужно рассмотреть три случая: когда производная положительна, равна нулю, и отрицательна.

При положительной производной поверхностное напряжение будет становиться всё больше на то же относительное расширение поверхности. Это нормальная ситуация для твердого тела. В случае производной = 0 атомы могут свободно перестраиваться между собой. Есть поверхностный избыток, но он может свободно выйти на поверхность, не требуя энергии. Характерно для жидкостей и аморфных тел. В кристаллах это же явление связано с большим выделением энергии (большое изменение межатомных связей(??)).
В случае отрицательной производной, начиная с некоторого момента, растяжение образца сопровождается снижением энергии. Это возможно в случае наличия дефектов в кристалле – перемещение края дефекта приводит к его более выгодному положению. Соответственно, это же условие выполняется при разрушении кристалла, т.е. кристалл разрушается потому, что существование двух кристаллов с двумя поверхностями энергетически выгоднее в таких условиях, чем одного кристалла с большим количеством дефектов.

Дата добавления: 2014-11-14; просмотров: 205; Нарушение авторских прав

Мы поможем в написании ваших работ!