
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Основы термодинамики поверхности
Уравнение Гиббса-Гюгема.
Равновесие однокомпонентной системы полностью характеризуется величиной внутренней энергии, которая является однозначной функцией энтропии, объема, и числа частиц. Кроме того, уравнение имеет вид…(1)
Приращение внутренней энергии, согласно термодинамике, будет описано …(2).
Величины в частных производных, как оказывается из экспериментальных данных, определяется из температуры, давления, и химического потенциала: dU = TdS – pdV + μdV. Кроме того, известно, что внутренняя энергия экстенсивна. Если взять постоянный коэффициент λ, и увеличить в λ раз энергию величин, то внутренняя энергия увеличится в λ раз: U (λS, λV, λμ) = λU (S, V, μ)
Внутренняя энергия зависит от этих величин линейно (ввиду указанных выше двух причин).
dU = TdS + SdT + pdV – Vdp + μdV + Ndμ.(-dU).То, что остальные величины равны 0 – и есть уравнение Гиббса-Гюгема: SdT – Vdp + Ndμ = 0.
Применение к поверхности.
Заключается в том, что наличие поверхности должно добавлять некоторую энергию, пропорциональную площади поверхности. U = TS – pV + μV + γA.
Уравнение Гиббса-Гюгема, соответственно, должно измениться следующим образом: dU = TdS – pdV + μdV. Приращение внутренней энергии опирается на приращение экстенсивной величины, значит, в приращении внутренней энергии будет участвовать дифференциал площади поверхности: dU = TdS – pdV + μdV + γdA =>SdT – Vdp + Ndμ + Adγ = 0.
Равновесие при любых конечных температуре и давлении в твердом теле сосуществует со своими парами. Приняли в рассмотрение модель, находящуюся в равновесии со своими парами. В ней мы можем выделить три области: твердое тело, пары, ограниченная область, где находится поверхность. В районе поверхности плотность вещества резко убывает. Состояние переходной области нас и интересует. Экстенсивные величины в таком случае можно определить следующим образом: экстенсивные величины будут составлять сумму этих величин по областям: S = S1 + S2 + SS; V = V1 + V2 + VS; N = N1 + N2 + NS. Поэтому, экстенсивные параметры для объемных фаз пропорциональны его объему:S1 = S1V1, S2 = S2V2, N1 = n1V1, N2 = n2V2. Такое утверждение для центральной модели, которую мы будем рассматривать… Вся модель замкнута, поэтому мы можем сказать, что число частиц, энтропия и объем постоянны, они могут переходить только частями в системе (∆S = 0 = ∆N = ∆V), поэтому изменение поверхностных параметров равно отрицательному изменению величин, связанных с объемом - ∆SS = -∆S1 - ∆S2, ∆Ns = -∆N1 - ∆N2, ∆VS = -∆V1 - ∆V2.
Важный момент – выбор границ (что считать областью) – здесь неоднозначен, впоследствии покажем, что неважно, как его сделать, всегда можно выбрать такую область, в которой будут определены все параметры, и они не будут зависеть от конкретного расположения границ.
11.10.14.
Рассмотрим эффект малых изменений поверхности, вызванных, например, растяжением. Будем предполагать при этом, что изменение энергии, связанное с этим процессом, описывается линейной теорией упругости. Тогда мы можем записать изменение энергии следующим образом, используя частные производные.
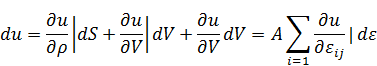
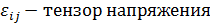
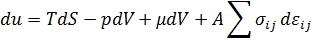
| <== предыдущая страница | | | следующая страница ==> |
| Решение уравнения Шредингера с таким потенциалом распадается на два независимых решения | | | Далее будем вводить уравнение Гиббса-Гюгема |
Дата добавления: 2014-11-14; просмотров: 197; Нарушение авторских прав

Мы поможем в написании ваших работ!