Многоканальная передача и многостанционный доступ

Пример 13. Можно ли серии импульсов вида

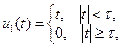
повторяющихся с периодом T>2τ, использовать в качестве канальных сигналов в трехканальной цифровой СПИ с амплитудной модуляцией?

Решение. Найдем элементы матрицы Грама для указанной системы функций (формула (6.2) [2])

Вычисляем определитель матрица Грама

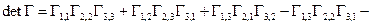
Определитель не равен нулю, следовательно, тройка импульсов, передаваемых одновременно, является линейно независимой. Итак, можно представленную систему использовать в качестве канальных сигналов.

Пример 14. Какая минимальная полоса частот требуется для аналоговой передачи по кабелю 12 телевизионных программ, если считать, что при ЧРК ширина защитного интервала составляет 20% от полосы, занимаемой канальным сигналом?

Решение. Минимальная полоса частот требуется при использовании АМ ОБП, когда модулированный сигнал занимает полосу 6,5 МГц, равную ширине спектра первичного ТВ сигнала. Тогда ширина защитного интервала равна 1,3 МГц. В итоге требуется 12 полос для передачи сигналов и 11 защитных интервалов, то есть 92,3 МГц.

Пример 15. Сколько телефонных сигналов можно передать в полосе частот 0,3 МГц, если осуществлять аналоговую передачу с АМ и использовать защитные частотные интервалы по 2 кГц?

Решение. При использовании АМ модулированный сигнал занимает полосу, равную удвоенной верхней граничной частоте первичного телефонного сигнала, то есть 6,8 кГц. С учетом защитного интервала на один канал потребуется полоса 8,8 кГц, и в полосе 300 кГц удастся разместить 34 канала.

Пример 16. Черно-белое изображение газетной полосы размером 42 см·59 см необходимо передавать за 2 мин с разрешением не хуже 13 точек/мм. Какой стандартный групповой тракт потребуется для аналоговой передачи с такой скоростью?

Решение. Количество элементов изображения равно Передачу необходимо вести со скоростью Минимальная полоса частот, которая требуется для передачи такого количества отсчетов, в соответствии с теоремой отсчетов равна 174,5 кГц. Передача возможна методом АМ с одной боковой полосой с использованием вторичного группового тракта (Приложение 4), имеющего полосу пропускания 240 кГц.

Пример 17. Определить необходимую битовую скорость передачи в 30-канальной цифровой многоканальной СПИ с ВРК, если первичный непрерывный сигнал в каждом канале имеет спектр, лежащий в полосе частот 0…10 кГц, а при его квантовании используются 512 уровней напряжения.

Решение. Для обеспечения 512 уровней напряжения требуется 9-разрядный АЦП, производящий преобразований в секунду. Тогда битовая скорость на выходе АЦП в одном канале составит 180 кбит/с. Минимальная битовая скорость передачи группового сигнала равна 180·30=5400 кбит/с, но реально скорость окажется несколько выше за счет того, что периодически нужно передавать синхросигналы.

Пример 18. Какая полоса частот потребуется для передачи 40 цифровых телефонных сигналов методом ВРК, если не передавать никаких синхросигналов и сохранить лишь 80 % полосы, занимаемой главным лепестком в спектре группового сигнала?

Полагать, что используется:

а) двоичная АМ;

б) двоичная ЧМ;

в) КАМ-256.

Решение. а) Скорость цифрового потока на выходе канального АЦП равна 64 кбит/с. При временном уплотнении необходимо обеспечить передачу со скоростью V = 64·40 = 2560 кбит/с. Главный лепесток в спектре АМ сигнала (см. рис. 2.14 [1]) занимает полосу Δf_гл = 2/τ = 2V, то есть 5,12 МГц, и для передачи потребуется полоса 5,12·0,8 = 4,096 МГц.

б) При применении ЧМ разнесение частот несущих для сигналов, соответствующих символам 0 и 1, обычно задают равным Δf_о = 1/τ = V = 2,56 МГц для обеспечения их ортогональности, тогда оба главных лепестка будут занимать полосу 7,68 МГц. После 20-процентного сокращения ширины спектра каждого из них получим полосу 6,656 МГц.

в) Каждый 256-ичный импульс в сигнале с КАМ-256 несет 8 бит, следовательно, можно его длительность увеличить в 8 раз. во столько же раз уменьшится ширина спектра сигнала по сравнению с АМ и составит 0,512 МГц.

Пример 19. Можно ли последовательности

+1, +1, –1, –1, +1, –1, –1, +1

+1, +1, –1, +1, +1, +1, +1, –1

–1, –1, –1, –1, +1, +1, +1, +1

–1, –1, +1, +1, +1, –1, –1, +1

использовать для внутриимпульсной модуляции четырех канальных сигналов в системе МДКР так, чтобы не возникало междуканальных помех?

Решение. Хотя необходимым условием отсутствия междуканальных помех является линейная независимость канальных сигналов, системы МДКР рассчитаны на использование ортогональных сигналов, для которых матрица Грама (формула (6.1) [2]) является диагональной.

Для проверки ортогональности канальных сигналов с внутриимпульсной ФМ, применяемых в системе МДКР, достаточно убедиться в ортогональности векторов с двоичными элементами, определяющих закон этой ФМ в каждом канале. Воспользуемся простым тестом: два таких вектора ортогональны, если они имеют ровно половину попарно совпадающих элементов. Видим, что все векторы попарно ортогональны, за исключением второго и четвертого, для которых Г_2,4 = –4, то есть этот набор сигналов использовать нельзя.

Пример 20. В четырехканальной системе МДКР для формирования канальных сигналов используются последовательности

+1, +1, –1, +1

+1, –1, +1, –1

+1, +1, –1, –1

+1, –1, –1, +1.

Найти отношение помеха/сигнал в каждом канале, если одновременно передаются все четыре сигнала.

Решение. Обозначим – двоичный элемент с номером j в модулирующей последовательности для сигнала k-го канала.

Тогда сигнал k-го канала при передаче информационного символа s_k, принимающего одно из двух равновероятных значений +1 или –1, состоит из четырех следующих один за другим и не перекрывающихся во времени радиоимпульсов прямоугольной формы

,

где f(t) – функция, описывающая форму элементарного радиоимпульса длительности τ. В итоге сигналы, соответствующие двум значениям информационного символа s_k, оказываются противоположными.

Выделение сигнала k-го канала осуществляется при помощи корреляционного приемника (2.27) [1]

где t_н и t_к = t_н +4τ – моменты начала и окончания составного сигнала на входе,

– сумма четырех сигналов на входе приемника.

Выполним интегрирование и получим

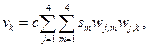
где – постоянная величина, равная энергии элементарного импульса.

Напряжение v_k на выходе приемника состоит из двух слагаемых:

1) полезного сигнала (при m = k) , энергия (квадрат модуля) которого неслучайна и всегда равна
Q_c = 16с²;

2) помехи равной сумме откликов приемника на остальные три сигнала.

Определим энергию помехи в каждом из каналов, полагая, что значения информационных символов в разных каналах независимы.

Для первого канала (k=1) имеем

Математическое ожидание напряжения помехи равно нулю вследствие равновероятности двух противоположных значений информационного символа s_k. Математическое ожидание квадрата модуля напряжения помехи

где – элемент матрицы Грама.

Величины , а значения 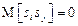при вследствие независимости информационных символов в разных каналах.

В итоге для энергии помехи в первом канале имеем

Аналогично для энергии помехи в остальных каналах имеем

Тогда отношение сигнал/помеха r для каждого из четырех каналов принимает следующие значения

r₁ = 0,75, r₂ = r₃ = r₄ = 0,25.

Разница в полученных результатах объясняется тем, что сигналы во втором, третьем и четвертом каналах взаимно ортогональны и поэтому не создают помех друг другу, а сигнал в первом канале не ортогонален всем остальным сигналам.

2.5 Синхронизация приемника цифровой СПИ

Пример 21. При передаче цифрового телефонного сигнала в канале без помех в начале каждого байта дополнительно передается символ 1 в качестве синхросигнала. Чтобы установить синхронизацию, селектор синхросигналов из принятой последовательности выбирает наудачу каждый девятый символ и, набрав таким образом 15 битов, выносит решение о том, является ли синхросигналом выбранная подпоследовательность. Найти вероятность того, что будет принято верное решение, полагая, что информационные символы независимы и с одинаковой вероятностью принимают значения 0 и 1.

Решение. Селектор примет верное решение, если произойдет одно из двух несовместных событий:

1) выбранная наудачу подпоследовательность является синхросигналом и, следовательно, состоит из одних единиц; вероятность такого события Р₁ = 1/9;

2) выбранная подпоследовательность не является синхросигналом (вероятность такого события составляет 8/9) и не состоит из одних единиц.

Вероятность того, что 15 информационных символов состоят из одних единиц, находим по формуле умножения вероятностей независимых событий . Следовательно, вероятность того, что они содержат хотя бы один ноль, равна (1–р) = 0,999969. Тогда вероятность события 2 равна

Р₂ = 0,999969·8/9 =0,888862.

В итоге вероятность того, что селектор примет верное решение, находим по формуле сложения вероятностей

Р = Р₁ + Р₂ = 0,111111 + 0,888862 = 0,999973.

Пример 22. Решить пример 21 при условии, что битовая вероятность независимых ошибок в симметричном канале равна р = 10^–3, а селектор выносит решение о наличии синхросигнала лишь в случае, когда количество единиц в выбранной подпоследовательности не менее 14.

Решение. Селектор примет верное решение, если произойдет одно из двух несовместных событий:

1) выбранная наудачу подпоследовательность является синхросигналом, а количество ошибок в ней не превышает единицы;

2) выбранная подпоследовательность не является синхросигналом и содержит менее 14 единиц.

Вероятность того, что в 15 принятых символах содержится не более одной ошибки, находим с использованием биномиальной формулы (3.57) [1]

Вероятность события 1 равна Р₁ = 0,111111·0,999896 = 0,111100.

Если два передаваемых символа равновероятны, то они останутся равновероятными и на выходе симметричного канала с ошибками. Тогда вероятность того, что в 15 принятых информационных символах содержится более одного нуля, также находим с использованием биномиальной формулы, положив р = 0,5

Вероятность события 2 равна Р₂ = 0,888889·0,999512 = 0,888455.

Селектор примет верное решение с вероятностью

Р = Р₁ + Р₂ = 0,111100 + 0,888455 = 0,999555.

Дата добавления: 2014-11-14; просмотров: 403; Нарушение авторских прав

Мы поможем в написании ваших работ!