Некоторые дополнительные определения на графах

Многообразие задач моделируемых графами порождает большое количество дополнительных определений и классификаций используемых в теории графов. Познакомимся лишь с небольшой их частью, необходимой нам в моделировании управления проектами.

Ребро e_i и вершина v_j называются инцидентнымиесли вершина v_j является одной из двух вершин, на которых базируется ребро e_i.

Два ребра графа имеющие общую вершину называются смежными.Две вершины графа имеющие общее ребро называются смежными

Путем P(v_a,v_b)={e_i | i=1,…n} между двумя вершинами v_a и v_b графа G(V,E) называется непустое упорядоченное подмножество ребер графа “ведущее” от вершины v_a к v_:. Интуитивно понятный термин “ведущее” означает что:

- e₁ инцидентно v_a,
- e_n инцидентно v_b,

- e_i смежна e_i-1 | i=2,…n.

Иногда “путь” называют “цепью”.

В приведенном ниже графе (Рисунок 2.1‑2) между вершинами v5 и v7 существует единственный путь состоящий из ребер e5 и e6:
P(v5,v7) = {e5,e6}.

На том же графе между вершинами v1 и v3 существует два пути:
P₁(v1,v3) = {e2} и P₂(v1,v3) = {e1,e3}.

А вот пути между вершинами v2 и v6 не существует (равно как и между v8 и v1 и многими другими парами).

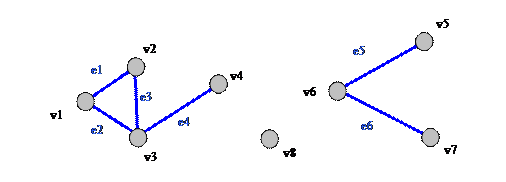
Рисунок 2.1‑2. Пример трехкомпонентного графа

Компонентом связности графа называется подграф - максимально полное подмножество вершин, между каждой парой которых существует путь, и множество ребер их соединяющих. Граф имеющий один компонент связности называется связным.

На приведенном выше примере (Рисунок 2.1‑2) граф имеет три компонента связности:
C₁=<{v1,v2,v3,v4},{e1,e2,e3,e4}>; C₂=<{v5,v6,v7},{e5,e6}>; C₃=<{v8}>.

Дата добавления: 2014-11-15; просмотров: 251; Нарушение авторских прав

Мы поможем в написании ваших работ!