Определение графа

Под графом (graph) понимают совокупность вершин (vertices) и соединяющих их ребер (edges). Вершины в графе часто называет узлами (nodes) – эти термины эквивалентны.

Более строго: графом G(V,E) называется совокупность двух множеств – множества V (множество вершин) и множества E (множество ребер), связанных следующим отношением. Каждый элемент множества Е определяет отношение (соединяет) между двумя элементами множества V.

Итак:

G(V,E) = <V,E>, E={e=(v1,v2)}

В качестве первого примера графа и его графической иллюстрации рассмотрим фрагмент схемы метрополитена. Этот фрагмент содержит 6 станций и 7 перегонов. Соответствующий ему граф (Рисунок 2.1‑1):

G(V,E)=<V,E>,
V={v1,v2,v3,v4,v5,v6},
E={e1=(v2,v4),e2=(v4,v5),e3=(v4,v6),e4=(v1,v5),e5=(v2,v1), e6=(v1,v3), e7=(v2,v5)}

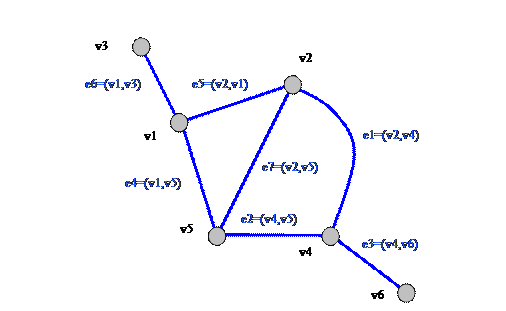
Рисунок 2.1‑1. Пример графа. Фрагмент схемы метрополитена.

Обратим внимание на несколько аспектов определения графа.

ü Множество вершин не может быть пустым. А вот множество ребер – может и в этом случае такой граф называют “нуль-графом”.

ü Множество ребер неупорядочено, то есть между ребрами нет дополнительных отношений

ü В определении ничего не говорится о дополнительных свойствах вершин и ребер и, в частности, нет понятия “координат узлов”. Поэтому расположение узлов (станций метрополитена) в той или иной точке на приведенном выше рисунке условно. Это именно схема, а не выполненная в масштабе карта.

Дата добавления: 2014-11-15; просмотров: 220; Нарушение авторских прав

Мы поможем в написании ваших работ!