
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лекция 8. Динамические ряды
8.1. Понятие и виды рядов динамики.
8.2. Правила построения рядов динамики и расчет их средних
уровней.
8.3. Показатели анализа рядов динамики.
8.1. Все общественные явления и процессы изменяются как в пространстве, так и во времени. Говоря языком статистики, они меняются как в статике, так и в динамике. Изучая изменение общественных явлений в статике, статистика строит ряды распределения, а во времени – ряды динамики.
Рядом динамики называют ряд чисел (числовых показателей), характеризующий изменение общественного явления во времени. Они состоят из двух элементов:
1. ряда уровней (численности, объема признака), которые характеризуют величину явления;
2. периодов или моментов времени, к которым относятся уровни ряда.
При графическом изображении уровни ряда динамики всегда откладываются по оси ОУ, периоды и моменты времени – по ОХ.
Динамические ряды строятся по различным общественным явлениям для того, чтобы стало возможным охарактеризовать процесс развития явления, показать основные пути, тенденции, темпы этого развития; с помощью динамических рядов выявляются те или иные закономерности развития общественных явлений.
В результате статистического наблюдения и подсчета итогов получаются абсолютные статистические показатели, из которых строят ряды динамики. Эти показатели называют уровнями динамических рядов.
В зависимости от характера общественного явления, от того, характеризуют ли уровни ряда процесс или состояние, различают два основных вида рядов динамики – интервальные и моментные. К первым, например, относятся данные о розничном товарообороте по кварталам. Итак, интервальным рядом динамики называется ряд статистических величин, каждая из которых характеризует процесс за определенный период времени (размер расходов на рекламу по годам и т.п.).
Уровни интервального ряда распределения зависят от величины интервала – отрезка времени, за который сообщаются сведения. Данные интервального ряда динамики обладают свойством суммирования, т.е. могут укрупнять или разукрупнять интервалы (квартал – полугодие – год). При этом показатели сохраняют свой экономический смысл, и по данным интервальных рядов строят ряды нарастающих итогов (чтобы видеть, как соблюдается запланированный рекламный бюджет и т.п.).
Моментный динамический ряд – ряд статистических величин, каждая из которых характеризует состояние явления на определенные моменты времени. Есть понятие интервала и здесь. Это промежуток времени между двумя датами, на которые сообщаются сведения. Каждый уровень моментного ряда не представляет итог работы, а только состояние явления на определенную дату. Например, различного рода запасы берутся по состоянию на квартальные даты: 1.01.2007, 1.04.2007, 1.07.2007 и т.п.
Моментные ряды динамики могут быть построены с равными и с разными интервалами. Кроме моментных и интервальных рядов на их основе строят ряды динамики производных величин, которые подразделяются на ряды динамики средних и относительных величин. По определению, ряд динамики средних величин – это ряд цифровых данных, характеризующих изменение средних размеров признаков общественных явлений во времени (средней зарплаты работников по годам и т.п.); ряд динамики относительных величин – это ряд числовых показателей, характеризующий изменение относительных размеров общественных явлений во времени.
8.2. При использовании и анализе динамических рядов прежде всего следует помнить о строгом соблюдении требований к их построению:
1. должна быть обеспечена полнота представления показателей (все уровни записываются последовательно и непрерывно);
2. данные динамического ряда должны быть точными, достоверными, научно обоснованными;
3. необходимо строго соблюдать периодизацию динамики, т.е. видеть не только количественные, но и качественные изменения общественных явлений и выделять такие периоды, где четко видно, как количественные изменения переходят в качественные (например, после дефолта 1998 г. и т.п.);
4. соблюдать сопоставимость показателей динамики, которая должна обеспечиваться методологией расчета;
5. должна быть сопоставимость по времени и территории (когда берется одинаковая территория или равная в зависимости от цели исследования), а также по кругу охватываемых объектов;
6. при анализе необходимо использовать систему динамических рядов.
В анализе и планировании важно знать не только составляющие уровни динамического ряда, но и средний уровень. Средние уровни в динамике называют хронологическими средними, в отличие от расчета средних варьирующих рядов. Это обобщающие статистические показатели динамического ряда. Они характеризуют то общее, типичное, что присуще развитию изучаемого общественного явления.
Методика расчета средних уровней динамических рядов имеет свои особенности, она зависит от вида динамического ряда.
Для интервального ряда расчет производится по формуле средней арифметической простой, т.к. уровни этого ряда обладают свойством суммирования:
 , так считается, например, среднемесячный товарооборот.
, так считается, например, среднемесячный товарооборот.
Средний уровень для моментного ряда исчисляется в зависимости от того, построен ли он с равными интервалами или нет. Если интервалы равные, то пользуются так называемой формулой средней хронологической:

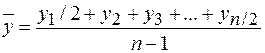 , т.е. в числителе сумма всех уровней ряда, причем первый и последний берутся в половинном размере, а в знаменателе число уровней ряда без одного.
, т.е. в числителе сумма всех уровней ряда, причем первый и последний берутся в половинном размере, а в знаменателе число уровней ряда без одного.
Если интервалы неравные, то используемые формулы зависят от того, имеется ли полная статистическая информация или неполная.
Если имеется полная статистическая информация, то средний уровень вычисляется по формуле средней арифметической взвешенной:
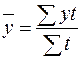 , где у – уровни динамического ряда, t – показатель времени.
, где у – уровни динамического ряда, t – показатель времени.
При полной информации мы располагаем всеми данными в любой момент от начала до конца периода (от даты изменения до следующей даты изменения).
При неполной информации расчет среднего уровня производится по формуле средней арифметической взвешенной из средних уровней между двумя смежными датами.
 , где
, где 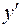 - это средняя между двумя смежными датами.
- это средняя между двумя смежными датами.
Пример.
Даны товарные запасы на несколько дат. На 1.01.07 – 12,0 , на 1.05.07 – 14,0 , на 1.10.01 – 15,0 и на 1.01.08 – 13,0 (все в тыс. руб.). Как видим, промежутки между датами разные: 4 месяца, 5 месяцев, 3 месяца. Необходимо найти средний товарный запас по приведенной выше формуле.
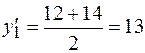 ;
;  ;
; 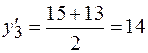
 (тыс.руб.)
(тыс.руб.)
Таким образом, среднемесячный товарный запас составил 13,9 тыс.руб.
8.3. В анализе динамических рядов важно выявить закономерность развития общественного явления. Для этого мы не только следим за абсолютными уровнями динамического ряда, но и за их изменением. Важно знать абсолютные изменения уровней и темпы этих изменений.
В анализе мы различаем начальный уровень, конечный и средний уровни ( 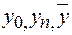 ). Уровень – это те абсолютные данные, которые составляют динамический ряд. Приведем пример в табличной форме.
). Уровень – это те абсолютные данные, которые составляют динамический ряд. Приведем пример в табличной форме.
| Годы | Розн. товаро- оборот (млрд руб.) | Абсол.прирост (млрд руб.) | Темпы роста в % | Темпы прироста в % | Абсол.значение 1 % прироста (в млн руб.) | |||
| Ежегод. | К 1999 | Ежег. | К 1999 | Ежег. | К 1999 | |||
| 155,2 | … | … | … | 100,0 | … | … | … | |
| 165,6 | 10,4 | 10,4 | 106,7 | 106,7 | 6,7 | 6,7 | ||
| 176,4 | 10,8 | 21,2 | 106,5 | 113,5 | 6,5 | 13,5 | ||
| 185,7 | 9,2 | 30,5 | 105,3 | 119,6 | 5,3 | 19,6 | ||
| 195,0 | 9,3 | 39,8 | 105,0 | 125,6 | 5,0 | 25,6 | ||
| 210,4 | 15,4 | 55,2 | 107,0 | 135,6 | 7,0 | 35,6 |
При анализе динамических рядов исчисляют:
1. абсолютный прирост (разность двух абсолютных уровней) – по цепной и базисной системе:
 по цепной системе ;
по цепной системе ;
 по базисной системе.
по базисной системе.
Между цепной и базисной системами абсолютных приростов существует взаимосвязь: последовательная сумма цепных приростов соответствует определенному базисному, а разность между каждым последующим и предыдущим базисным приростом дает соответствующий цепной абсолютный прирост (см. табличный пример).
Абсолютный прирост выражает абсолютную скорость изменения уровней динамического ряда, относительную же скорость, интенсивность изменения динамического ряда характеризуем темпами роста.
2. Темп роста – это отношение двух абсолютных уровней по цепной или базисной системе. Темпы роста могут быть выражены в коэффициентах или процентах:
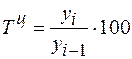 темп роста по цепной системе в процентах;
темп роста по цепной системе в процентах;
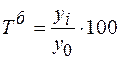 темп роста по базисной системе в процентах.
темп роста по базисной системе в процентах.
Между цепной и базисной системами коэффициентов существует следующая взаимосвязь: произведение цепных коэффициентов дает соответствующий базисный коэффициент. Частное от деления каждого последующего базисного коэффициента на предыдущий дает промежуточный цепной коэффициент. Знание этого необходимо для нахождения недостающих показателей (переход от цепной системы к базисной и наоборот).
3. Темп прироста – разница между темпом роста и базой (или отношение абсолютных приростов к соответствующим абсолютным уровням). Если темп выражен коэффициентом, то за базу принимается единица, если процентом – то 100:
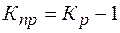 ;
; 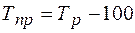 , это первый способ расчета, или
, это первый способ расчета, или
 ;
; 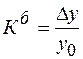 , это второй способ расчета для цепной и базисной систем соответственно (для выражения в процентах достаточно умножить на 100).
, это второй способ расчета для цепной и базисной систем соответственно (для выражения в процентах достаточно умножить на 100).
4. Синтетический показатель, объединяющий относительные и абсолютные показатели, – абсолютное содержание или значение одного процента прироста. Оно рассчитывается делением абсолютных приростов на темпы прироста, рассчитанных только по цепной системе (для базисной системы не рассчитываются, т.к. теряют экономический смысл).
1% прироста =  , например, по данным нашей таблицы для 2000 года 1% прироста =
, например, по данным нашей таблицы для 2000 года 1% прироста = 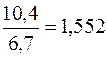 (млрд руб.) или 1552 млн руб. – см. табл.
(млрд руб.) или 1552 млн руб. – см. табл.
При анализе различают следующие основные типы динамических рядов:
1. если происходит рост значений уровней динамического ряда – это ряд с тенденцией к росту;
2. если уровни динамического ряда изменяются мало – это стабильные динамические ряды;
3. если налицо снижение значений уровней – тенденция к падению уровней (падающие абсолютные уровни).
Бывает, что по абсолютному изменению и уровням динамического ряда нельзя сделать вывод о закономерности развития (уровни и изменения то растут, то снижаются). Тогда нужно выявить тенденцию уровней динамического ряда – произвести выравнивание.
Расчет средних темпов осуществляется по формуле средней геометрической:
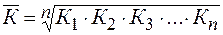 , где n – число коэффициентов,
, где n – число коэффициентов, 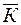 - средний коэффициент, или по другой формуле
- средний коэффициент, или по другой формуле 
 , если
, если 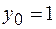 , то применяется следующая формула
, то применяется следующая формула

Таким образом, средние темпы роста рассчитываются с использованием цепных или базисных индексов в зависимости от конкретных имеющихся данных.
Контрольные вопросы
1. Дайте понятие ряда динамики.
2. Из каких двух элементов состоят ряды динамики?
3. Чем отличаются моментные и интервальные ряды динамики?
4. Какие требования соблюдаются при построении динамических рядов?
5. Какие виды средних применяются для рядов динамики?
6. Чем различается выбор средних для интервального и моментного ряда?
7. Дайте характеристику показателей анализа ряда динамики.
8. Приведите основные формулы для анализа динамических рядов.
9. Как рассчитываются средние темпы роста динамического ряда?
Библиографический список
1. Бадрызлов В.А., Лантушенко Л.С. Общая теория статистики: учеб. пособие. – Омск: Изд-во ОмГТУ, 2001.
2. Громыко Г.Л. Теория статистики: практикум. – М.: ИНФРА-М, 2006.
3. Едронова В.Н., Едронова М.В. Общая теория статистики: учеб. для студентов вузов. – М.: Юристъ, 2001.
4. Потуданская В.Ф. Статистика. Основы общей теории. – Омск: Изд-во ОмГТУ, 2005.
5. Рафикова Н.Т. Основы статистики: учеб. пособие для вузов. – М.: Финансы и статистика, 2005.
6. Сиротина Т.П. Экономика и статистика предприятия: учеб. пособие. – М.: МЭСИ, 2002.
7. Статистика: курс лекций / В.Г. Долженкова и др.; под ред. В.Г. Ионина. – Новосибирск: Изд-во НГАЭиУ; М.: ИНФРА-М, 2000.
8. Статистика рынка товаров и услуг: учеб. для студентов вузов / И.К. Беляевский и др.; под ред. И.К. Беляевского. – М.: Финансы и статистика, 2002.
9. Статистический учет и отчетность при переходе на статистику предприятия: сборник научн. трудов. – Новосибирск: СибУПК, 2001.
10. Теория статистики: учеб. для вузов / Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 2006.
11. Экономика и статистика фирм: учеб. для студентов вузов / В.Е. Адамов и др.; под ред. С.Д. Ильенковой. – 2-е изд. – М.: Финансы и статистика, 1998.

| <== предыдущая страница | | | следующая страница ==> |
| Классификация индексов производится по нескольким признакам | | | ДНК. ИСТОРИЯ ОТКРЫТИЯ. СОВРЕМЕННЫЕ ПРЕДСТАВЛЕНИЯ |
Дата добавления: 2014-11-20; просмотров: 555; Нарушение авторских прав

Мы поможем в написании ваших работ!