Классификация индексов производится по нескольким признакам

По признаку охвата индексируемых экономических явлений, т.е. в зависимости от того, характеризуем ли мы все сложное явление или его части, отдельные элементы, индексы делятся на общие, групповые или частные и индивидуальные. Общие – это сводные индексы, методика вычисления их и групповых индексов одинакова, поэтому можно рассматривать групповые как частный случай сводных и различать две основные категории индексов – общие и индивидуальные.

По форме построения, способу исчисления общие индексы делятся на агрегатные (по методу сумм) и средние из индивидуальных: средние арифметические (по методу средних величин) и средние гармонические.

По базам сравнения – базисные (с постоянной базой сравнения) и цепные (с переменной базой сравнения). Они могут быть как индивидуальными, так и общими.

По характеру веса: с постоянными и переменными весами.

По объекту исследования: индексы качественных и количественных, объемных признаков. Индексы качественных признаков – индексы цен, себестоимости, производительности труда. Индексы количественных признаков – индексы физического объема товарооборота, объема выпуска продукции, объема общих затрат и т.п.

Основные категории индексов – индивидуальные и общие. Индивидуальные – относительные показатели, характеризующие изменение величины элемента одного какого-либо сложного явления (изменение цены одного товара и т.п.). Общие индексы – относительные показатели, характеризующие изменение сложного явления, состоящего из элементов, непосредственно не соизмеримых.

Общие индексы в отличие от индивидуальных дают обобщающую характеристику изменения сложного явления или какой-то его части.

В индексе различают два периода – базисный и отчетный (текущий). С базисным периодом сравниваем отчетный; им соответствуют значки «0» и «1». Буквой i обозначается индивидуальный индекс; p – цена, price ; q – количество; z – себестоимость ; t – затраты труда на единицу продукции.

Соответствующие индексы равны:

; ;

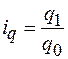Есть только одно исключение: , т.к. со временем затраты труда на изготовление единицы продукции не увеличиваются, а сокращаются ( со снижением затрат производительность труда растет – обратная зависимость).

7.3. Для общих индексов необходимо решить следующие задачи:

1. правильно выбрать элементы сложного явления с точки зрения поставленной задачи анализа;

2. найти правильный способ соизмерения тех величин, которые входят в данный индекс, т.е. при построении общих индексов необходимо правильно выбрать индексируемую величину и соизмеритель или вес.

Пример.

Необходимо соизмерить цены за разные периоды времени. Если это цены на разные товары, то с экономической точки зрения цены непосредственно сравнивать нельзя. Для соизмерения цены представляем как стоимости:

При выборе веса исходим из сущности социально-экономических явлений, т.е. мы должны получить не только относительное изменение цен на исследуемые товары, но и реальную сумму экономии или перерасхода денежных средств населением от изменения цен. Эта реальная величина может быть получена, если в качестве веса возьмем количество отчетного периода:

- товарооборот отчетного периода ;

- товарооборот отчетного периода в ценах базисного периода.

Правило построения общего базиса следующее:

1. веса индексов фиксируются на одном и том же уровне, но вес небезразличен к исследуемому показателю, он влияет на величину индекса;

2. исходя из существа общественных явлений для признаков качественных в веса всегда берутся количества отчетного периода, если же индексируется количественный признак, то весом является качественный признак базисного периода.

Это правило уже было учтено выше при построении общего индекса цен : за вес здесь было взято количество отчетного периода, т.к. индексируемый признак – цена – качественный . Если же мы возьмем общий индекс количества проданного товара, то за вес мы берем качественный признак (цену) базисного периода:

В то же время для расчета изменений в уровне отчетных и базисных показателей берется следующая формула индекса товарооборота:

Здесь, в отличие от предыдущих индексов, как числитель, так и знаменатель являются не условными, а реальными величинами. В числителе находится величина товарооборота отчетного периода, в знаменателе – величина товарооборота базисного периода.

Чтобы понять, как изменился товарооборот и за счет чего, необходимо разложить влияние по факторам. Для этого нужно представить себе взаимную связь между исследуемыми показателями, каковыми являются количество проданного товара и его цена. Взаимная связь между индексами цен и количества проявляется точно так же, как и между самими общественными явлениями, для которых исчисляются индексы: товарооборот равен цене, умноженной на количество проданного товара, цена равна товарообороту, деленному на количество, и т.п.

Отсюда ; ; .

Взаимосвязь между абсолютными величинами находится через сложение и вычитание числителей и знаменателей соответствующих индексов. Так, общая сумма изменения товарооборота составляет:

В том числе за счет изменения цен:

В том числе за счет изменения количества проданных товаров:

Взаимосвязь между индексами необходима:

1. чтобы вычислить влияние факторов на динамику общего показателя;

2. чтобы рассчитать на основе имеющихся двух показателей недостающий третий показатель.

Все рассмотренные индексы – индексы агрегатной формы или составные индексы, составленные из элементов. Дадим им определение. Агрегатный индекс – это отношение суммы отчетных значений индексируемого признака, взвешенных на соответствующие значения признака веса, к сумме базисных значений индексируемого признака, взвешенных по тем же значениям признака веса.

Агрегатная форма – основная форма исчисления общих индексов, она применяется более чем в девяти из десяти случаев использования индексов. Особенность агрегатной формы в том, что в ней наиболее наглядно и полно раскрывается экономический смысл индекса, легко читается числитель и знаменатель индекса. В агрегатной форме легко выявляется роль и влияние отдельных факторов на динамику изучаемого явления, и эта форма наиболее проста в расчетах. Так, агрегатная форма индекса цен применяется в том случае, если имеются данные о ценах и количествах по отдельным товарам в отчетном и базисном периодах.

В то же время часто известен рост цен по отдельным товарам, т.е. индивидуальные индексы цен. Имея подобные данные, мы можем вычислить общий индекс цен по средним из индивидуальных, которые выступают как производные от агрегатных индексов; они должны быть тождественны агрегатным индексам. Различают среднюю гармоническую и среднюю арифметическую формы общих индексов. Для получения общих индексов необходимо иметь агрегатную форму (формулу) соответствующего индекса и индивидуальные индексы.

Пример.

Имеются общий и индивидуальные индексы цен.

Общий ; индивидуальный .

Отсюда ; ; последнее выражение напоминает 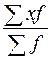, т.е. среднюю арифметическую. С другой стороны, найдем , тогда , что в свою очередь напоминает

, т.е. формулу средней гармонической взвешенной.

В чем же сходство и различие двух форм общих индексов? Сходство в том, что они тождественны друг другу: числитель и там, и там – это товарооборот отчетного периода, а знаменатель – товарооборот отчетного периода в ценах базисного. Различие же имеется в форме построения.

Практически для выбора той или иной формы индекса имеется правило: если в агрегатной форме реальной величиной является числитель, то ее преобразуют в среднюю гармоническую, весом которой является слагаемое числителя агрегатной формы. Так, для индекса цен необходима средняя гармоническая форма, когда мы оставляем числитель без изменения, а преобразуем знаменатель.

Если же реальной величиной является знаменатель, то необходимо преобразование в среднюю арифметическую, весом которой является слагаемое знаменателя агрегатной формы. Это мы можем наблюдать, когда имеем дело с индексом количества:

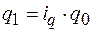; ; , что соответствует формуле средней арифметической взвешенной.

7.4. Когда нам необходимо сравнить показатели не двух периодов, а более, нас интересуют цепные и базисные индексы. Их различие в базах сравнения. Цепные индексы определяются при нахождении отношений уровней каждого последующего периода к каждому предыдущему. Базисные индексы – это отношения уровней каждого последующего периода к одному уровню, принятому за базу для сравнения.

Как цепные, так и базисные индексы могут быть индивидуальными и общими. Между индивидуальными индексами существует следующая взаимосвязь: произведение цепных индексов равно соответствующему базисному индексу, а частное от деления последующего базисного индекса на предыдущий соответствует определенному цепному индексу.

Пример.

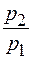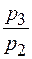, , и т.п. – это цепные индексы цен ;

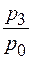, , и т.п. – это базисные индексы цен.

Взаимосвязь индексов можно проиллюстрировать формулами:

, т.е. произведение цепных индексов равно базисному, в данном случае произведение трех последовательных цепных дало третий базисный индекс;

, т.е. частное от деления второго по порядку базисного индекса на первый дало второй цепной индекс.

При построении общих индексов возникает проблема веса, т.к. взаимосвязь цепных и базисных систем возможна только при наличии постоянного веса. При построении общих индексов одной системы веса могут быть постоянными или переменными, выбор веса зависит от сущности выбранного явления, от того, количественный или качественный признак индексируется в системе. Например, цена – качественный признак, цены складывать нельзя, вес в числителе и знаменателе индекса цен должен быть одним и тем же. В этом случае в качестве веса берется количество последнего используемого периода и применяются формулы:

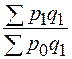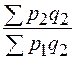; ; и т.п. для цепной системы ;

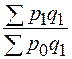; ; и т.п. для базисной системы.

Таким образом, при построении системы индексов качественных признаков вес в системе должен быть переменным, т.е. на уровне соответствующего периода. При построении системы индексов количественных признаков вес берется на уровне базисного периода и является постоянным.

Для качественных признаков ставится задача не только измерения относительного изменения во времени, но и определения экономического эффекта или потерь от их изменения. Для количественных признаков ставится задача изучения динамики количества, поэтому вес фиксируется постоянный.

Контрольные вопросы

1. Дайте определение понятию индекса.

2. Чем индекс в статистике отличается от других относительных величин?

3. Какие два признака включает в себя индексная система?

4. Каковы задачи и значение индексов?

5. Приведите классификацию индексов.

6. Чем отличаются индивидуальные и общие индексы?

7. Как осуществляется выбор веса в общих индексах?

8. Опишите взаимосвязь между основными общими индексами.

9. Приведите формулы агрегатных индексов и средних из индивидуальных.

10.В чем различие и взаимосвязь цепных и базисных индексов?

Дата добавления: 2014-11-20; просмотров: 398; Нарушение авторских прав

Мы поможем в написании ваших работ!