
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Командаconnectимеет формат
sysc= connect(sys, Q, inputs, outputs)
и используется для формирования уравнений состояния сложных систем. Предполагается, что система управления состоит из ряда подсистем, каждая из которых описывается системой уравнений тина (1), (2), сложным образом связанных между собой. Вначале выполняется командаappend,которую уже рассматривали раньше, с этими подсистемами, в результате чего образуется система sysподсистем, не связанных между собой, а затем уже выполняется команда connect. В этой команде inputsиoutputsecтьвекторы, содержащие индексы тех входов и соответственно выходов sys,которые будут назначены как входы и выходы окончательной системыsysc. Матрица Qсодержит указания на соединения выходов со входами sys. Она состоит из ряда строк, первый элемент которых указывает на индекс входа, а остальные элементы указывают индексы выходов, с которыми этот вход соединен по схеме суммирования, причем, если какой-либо выход вычитается, он указывается со знаком минус. Все строки должны иметь одинаковое число элементов, недостающие позиции заполняются нулями. Эта команда не работает при наличии запаздывания.
Пример. Привод вращающейся печи (Kiln) осуществляется от двух двигателей, имеющих равные моменты инерции J1, через эластичные муфты с коэффициентами жесткости С1 и С2, создающими на валах двигателей упругие моменты My1, My2. Моменты двигателей обозначены Md1, Md2, их скорости вращения ωd1, ωd2. Вращающаяся печь имеет момент инерции J2 и скорость вращения ωm (рис. 17). Все величины приведены к скорости вращения валов двигателей. Упругий момент пропорционален разности угловых положений вала двигателя и печи. Регулирование вращения осуществляется интегро-пропорциональным регулятором скорости, на входе которого сравниваются заданное значение скорости ωrefи скорость вращения первого двигателя Выход регулятора задает моменты двигателей. Будем пренебрегать динамикой регуляторов момента двигателей, так что фактические моменты двигателей равны заданным. Кроме того, момент второго двигателя корректируется в функции разности скоростей вращения двигателей. Смысл этого рассмотрим ниже.
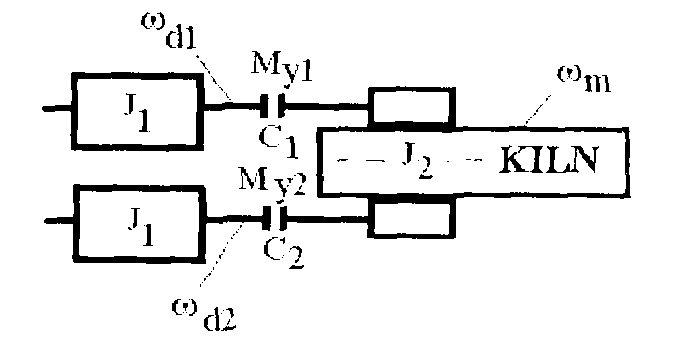
Рис. 17. Двухдвигательный электропривод вращающейся печи
Всю систему можно представить состоящей из 4-х подсистем (рис. 18), где первые две – это двигатели с полумуфтами, третья – вращающаяся печь, четвертая – регулятор скорости. На основании уравнений (3)-(5) можно записать:
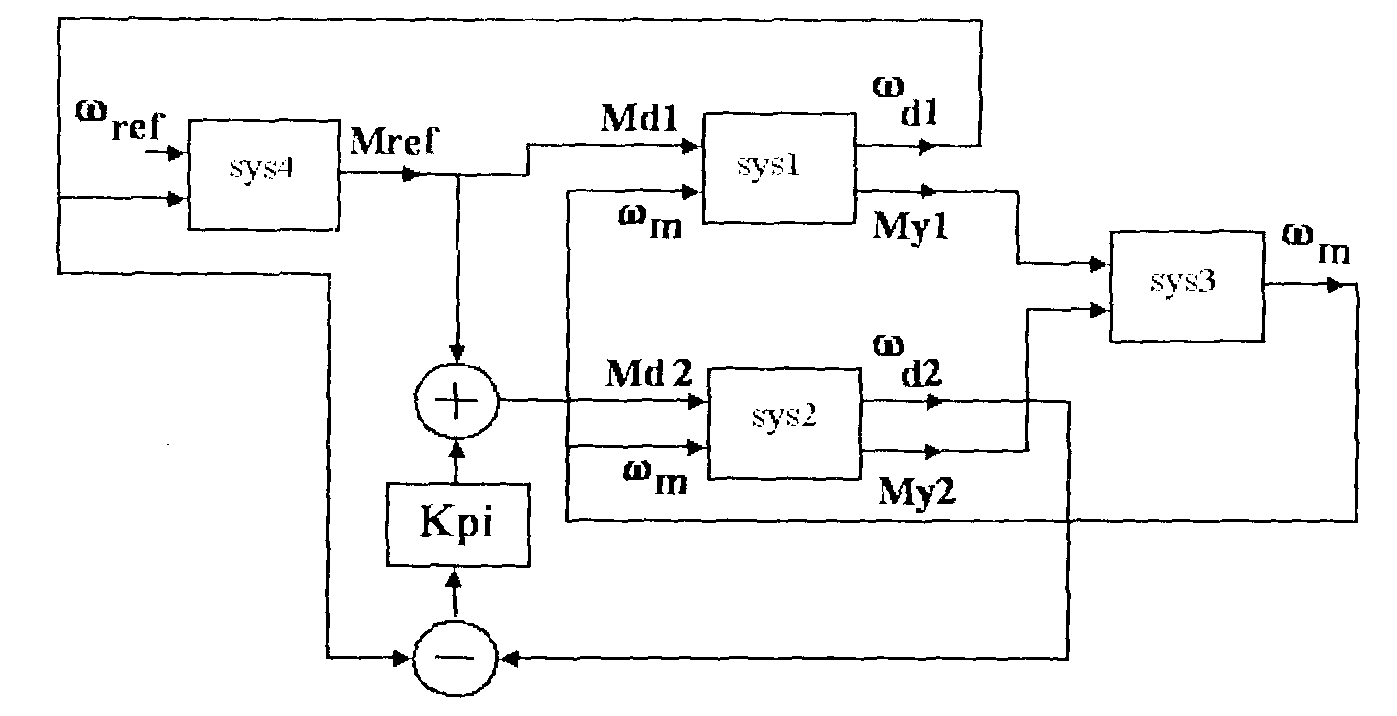
Рис. 18. Структурная схема системы электропривода вращающейся печи
sys1:
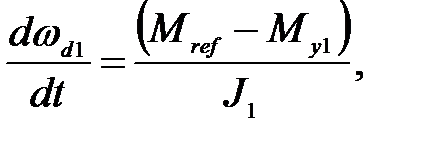 (19)
(19)
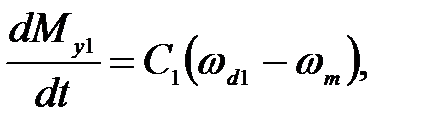 (20)
(20)
sys2:
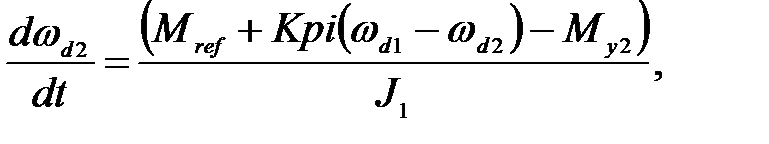 (21)
(21)
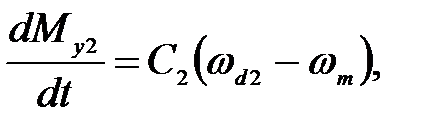 (22)
(22)
sys3:
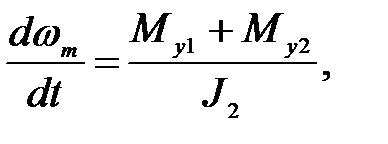 (23)
(23)
sys4:
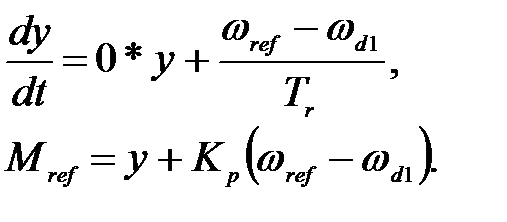 (24)
(24)
Уравнения (24) дают передаточную функцию регулятора Wr, приведенную в (15). Создадим файл (П. 8), предполагая, что все состояния измеримы, т. е. матрицы С– единичные.
Tr= 1/350; Kp = 160; J1 = 21.5; J2 = 2*7; С2 = 243*0.7; С1=243;
Kpi= 120;%Kpi=0;
a1= [0 -1/J1;C1 0]; b1 = [1/J1 0;0 -С1];с1 = [1 0;0 1];
sysl= ss(a1, b1, с1, 0);
set(sys1, 'StateName',{'Wd1;'Му1'},'InputName',...
{'Md';'Wm'},'OutputName', {'Wd1';'Му1'});
a2 = [0 -1/J1; C2 0]; b2 = [1/J1 Kpi/J1 0;0 0 -C2];
sys2 =ss(a2, b2, c1, 0, 'StateName',{'Wd2';'My2'},...
'InputName', {'Md2';'delw';'Wm'}, 'OutputName', {'Wd2';'My2'});
a3 = 0;b3 = [1/J2]; c3= [1];
sys3=ss(a3, b3, c3, 0, 'StateName', 'Wm',...
'InputName', 'My1+My2', 'OutputName', 'Wm');
b4 =[1/Tr -1/Tr]; d4=[Kp -Kp];
sys4 =ss(a3, b4, c3, d4, 'InputName',{ 'Uref'; 'Wd1'},...
'OutputName', 'Ureg');
sys= append(sys1, sys2, sys3, sys4);
Q =[1 6 0; 2 5 0; 3 6 0; 4 1 -3; 5 5 0; 6 2 4; 8 1 0];
Inputs = [7]; outputs = [1 3];
sysc= connect(sys, Q, inputs, outputs)
step(sysc, 4)
grid(П. 8)
Вначале создаются описанные выше четыре подсистемы. Затем они объединяются в одну систему командойappend.Система sysимеет матрицы (приKpi= 120, С1 = С2):
| a = | Wd1 | My1 | Wd2 | My2 | Wm | ? |
| Wd1 | -0.0465 | |||||
| My1 | ||||||
| Wd2 | -0.0465 | |||||
| My2 | ||||||
| Wm | ||||||
| ? |
| b = | Md | Wm | Md2 | delw | Wm | My1+My2 | Uref | Wd1 |
| Wd1 | 0.0465 | |||||||
| My1 | -243 | |||||||
| Wd2 | 0.0465 | 5.58 | ||||||
| My2 | -243 | |||||||
| Wm | 0.0714 | |||||||
| ? | -350 |
| c = | Wd1 | My1 | Wd2 | My2 | Wm | ? |
| Wd1 | ||||||
| My1 | ||||||
| Wd2 | ||||||
| My2 | ||||||
| Wm | ||||||
| ? |
| d = | Md | Wm | Md2 | delw | Wm | My1+My2 | Uref | Wd1 |
| Wd1 | ||||||||
| My1 | ||||||||
| Wd2 | ||||||||
| My2 | ||||||||
| Wm | ||||||||
| Ureg | -160 |
Назначим вход объединенной системы ωref и выходы ωd1 и ωd2 (первый и третий). Соответственно сформированы векторы inputsи outputs. Остальные входы связаны с выходами так, как это следует из приведенных выше уравнений, что и зафиксировано в матрицеQ.После выполнения командыconnectполучаем syscв виде:
| a = | x1 | x2 | x3 | x4 | x5 | x6 |
| x1 | -7.44 | -0.0465 | 0.0465 | |||
| x2 | -243 | |||||
| x3 | -1.86 | -5.58 | -0.0465 | 0.0465 | ||
| x4 | -243 | |||||
| x5 | 0.0714 | 0.0714 | ||||
| x6 | -350 |
| b = | Uref |
| x1 | 7.442 |
| x2 | |
| x3 | 7.442 |
| x4 | |
| x5 | |
| x6 |
| c = | x1 | x2 | x3 | x4 | x5 | x6 |
| Wd1 | ||||||
| Wd2 |
d =0.
На рис. 19 показаны переходные процессы при единичном скачке задания при С1= С2и Kpi= 0. Скорости обоих двигателей изменяются одинаково. Причем переходный процесс такой же, как на рис. 12, так как система, процесс в которой показан на рис. 12, представляет собой «половину» рассматриваемой системы. Однако, системы syslи sys2 могут различаться, впервую очередь, из-за различных люфтов в передачах, не
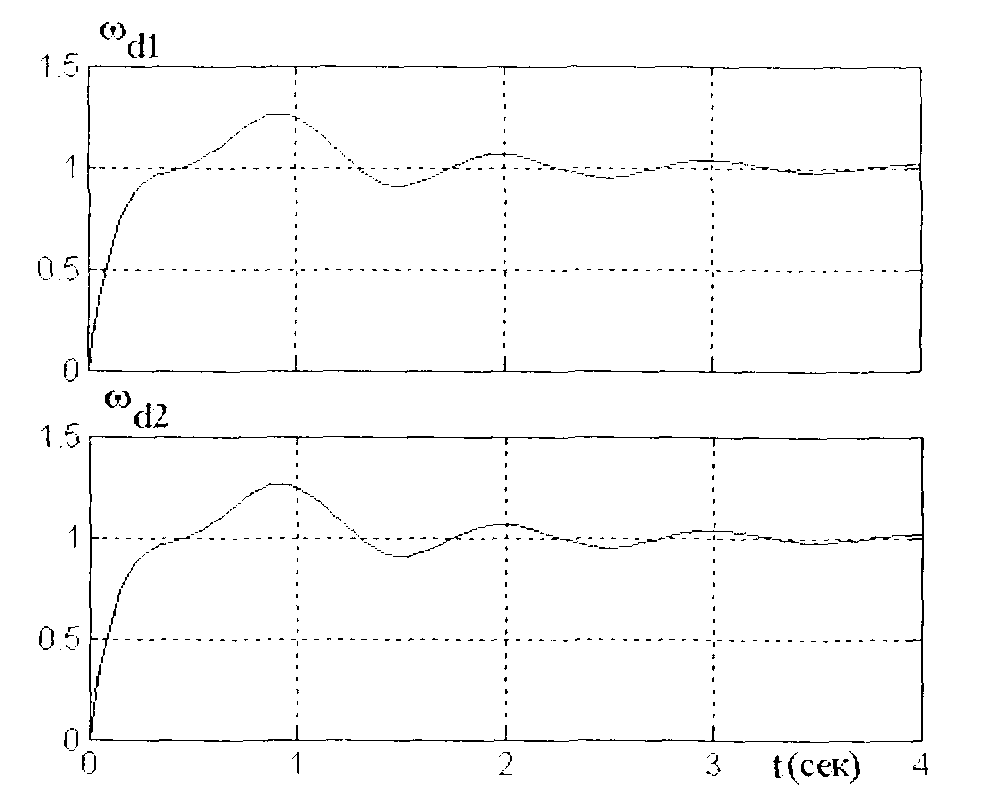
Рис. 19. Переходные процессы в электроприводе
при одинаковых параметрах эластичных муфт
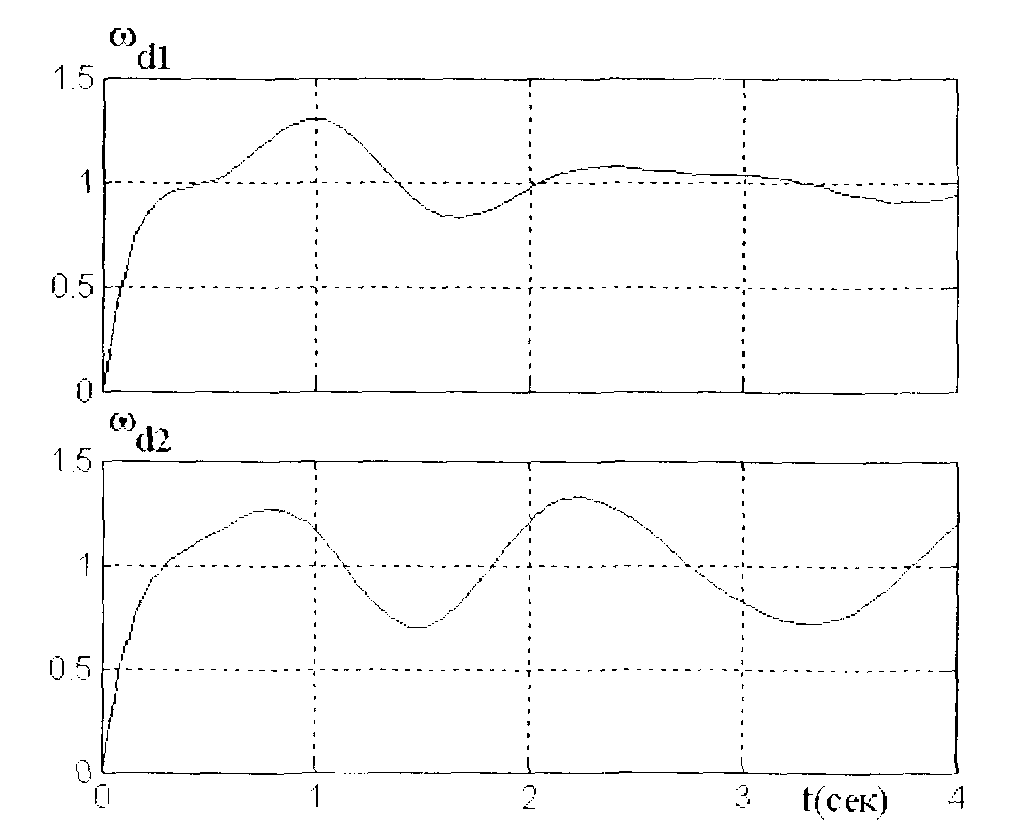
Рис. 20. Переходные процессы при различных муфтах
и отсутствии коррекции скорости
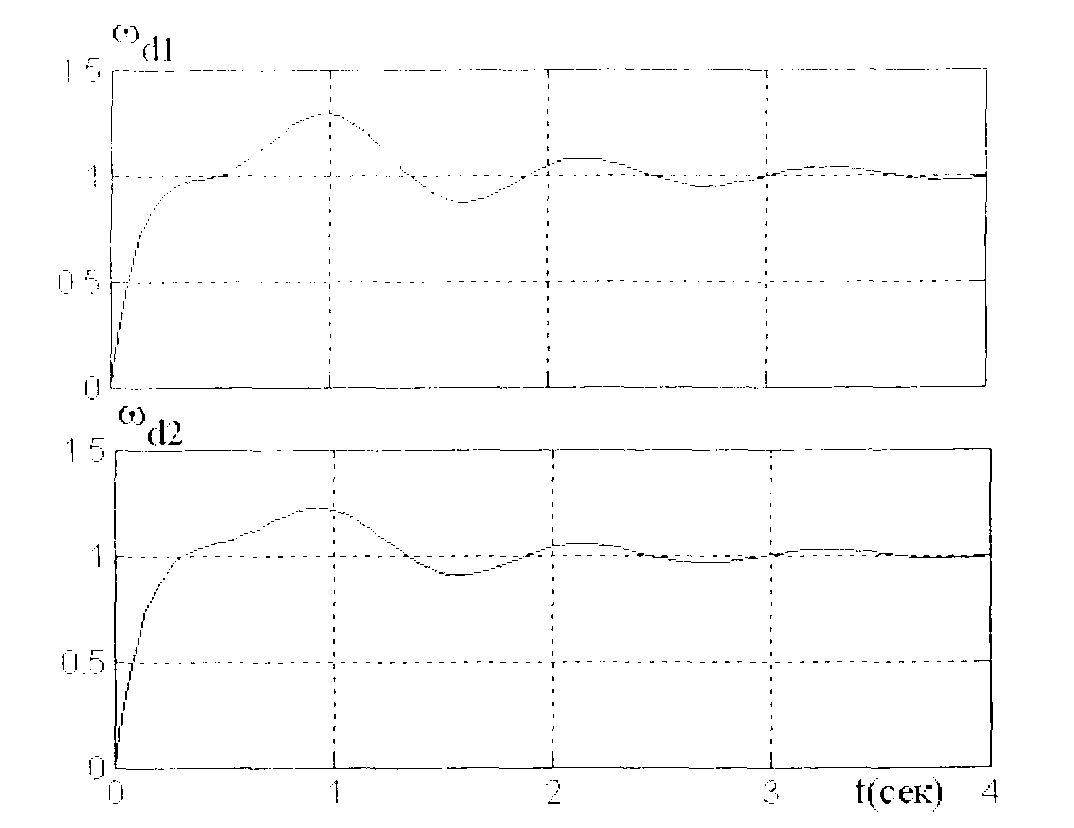
Рис. 21. Переходные процессы при различных муфтах
и включенной коррекции скорости
учитываемых в рассматриваемых линейных системах, а также из-за разности коэффициентов упругости обеих муфт, вызванной различным износом упругих элементов муфт. На рис. 20 показан процесс при С2 = 0.7С1. Видно заметное увеличение колебательности. На рис. 21 показан тот же процесс, но при введении воздействия по разности скоростей вращения обоих двигателей с коэффициентом пропорциональности Kpi= 120. Видно, что процесс близок к таковому в симметричной системе (рис. 19).
Иногда возникает необходимость в выделении части входов и выходов системы и в оперировании с такой усеченной подсистемой как с самостоятельной единицей. Для этой цели можно использовать обычные приемы выделения подматриц, используемые в системе MATLAB. Например, из MIMOсистемы sysс несколькими входами и выходами можно извлечь SISOсистему, соответствующую первому входу и второму выходу, командой
subsys= sys(2,1)
(первый индекс выход, второй – вход), подсистему с выходом 2 и входами 1и2 командой
subsys= sys(2, 1:2),
подсистему, сохраняющую все выходы от входа 1 командой
subsys= sys(:,1),
подсистему. сохраняющую все входы и только 1и 3 выходы командой
subsys= sys([1 3], :).
В системе можно добавлять входы. Если, например, в системе с одним выходом и двумя входами, образованной командой Н= [h11h12], записать
s = tf('s')
sys = [H, 1/s],
то получим систему с тремя входами, причем передаточная функция от третьего входа к выходу равна l/s.
В системе можно также удалить некоторые входы или выходы. Если, например, требуется удалить второй и третий входы, выполняется команда:
sys(:,2:3) = [].
Использование команд оперирования с матрицами системы MATLABчасто может быть эффективным средством для построения сложной системы. Рассмотрим, например, задачу из руководства по использованию ControlSystemToolbox. Дана схема, приведенная на рис. 22, Н1, Н2,Н3– передаточные функции,G–скалярный коэффициент усиления,F– передаточная функция фильтра. Необходимо получить систему, имеющую три входа: u, w1, w2 и два выхода: yf, f. Для этой цели оказывается достаточно трех команд:
Рх = append([ss(H1), Н2], НЗ)
Рх = [-G G;1 1]*Рх
Pxd= append(F, 1)*Рх.(П. 9)
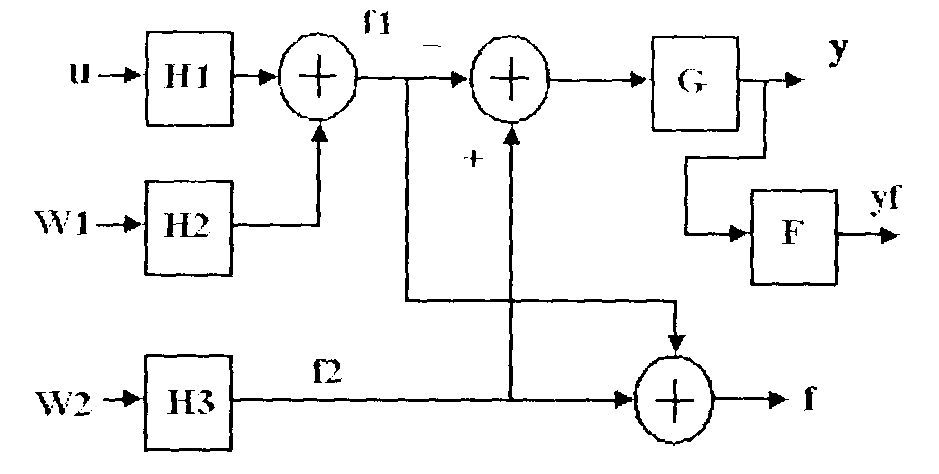
Рис. 22. Использование команд работы с матрицами
Первая команда сначала образует систему с двумя входами u, w1и выходом f1, затем добавляет к ней систему Н3 с выходом f2. При этом также осуществляется преобразование одной из систем, а именно Н1 в систему SS, так как в таком виде точность максимальна. В соответствии с (14) и все дальнейшие преобразования будут представлены в таком же виде. Вторая команда выполняет операцию
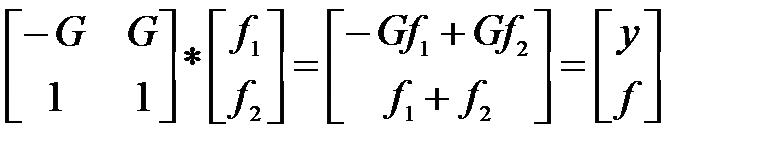
а третья команда фильтрует первый выход и пропускает без изменения второй. Надо сказать, что применение такого рода cocтавных команд требует определенных навыков, и может быть рекомендовано только после освоения основных, более прозрачных команд, приведенных в табл. 1.
До настоящего времени мы рассматривали команды, которые предлагает ControlSystemToolbox, но RobustControlToolboxтакже предлагает команды взаимосвязи систем. Например, команда
[ssc] = interc(sys, M, N, F)
присоединяет к системе sysпостоянные матрицы М, N, Fпо схеме рис. 23. Предполагается, что sysимеет вид (1), (2), в результате выполнения команды sscбудет иметь такой же вид, но с матрицами
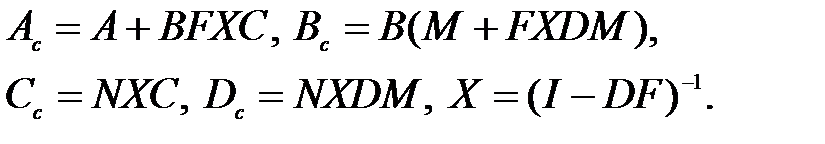 (25)
(25)
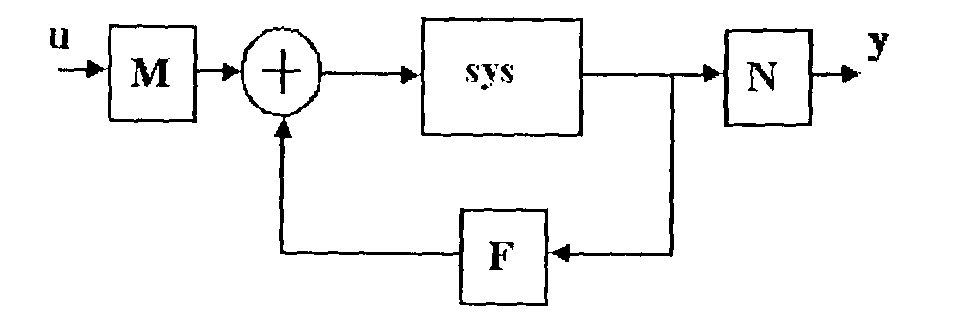
Рис. 23. Для выполнения команды interc
| <== предыдущая страница | | | следующая страница ==> |
| Соединения моделей | | |
Дата добавления: 2014-11-20; просмотров: 310; Нарушение авторских прав

Мы поможем в написании ваших работ!