
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Соединения моделей
Обычно система регулирования состоит из ряда подсистем: объект регулирования, датчики, регулятор, фильтры и др. Каждая из этих подсистем описывается одним из четырех рассмотренных выше типов. Для получения модели всей системы их нужно соединить между собой в соответствии с общей схемой. Для этой цели в ControlSystemToolbox предусмотрен ряд команд. Рассмотрим их подробно (табл. 1).
Команды 8 и 9 записываются как
sys3 = [sys1, sys2]иsys3 = [sys1; sys2]
соответственно. Если для sys1 y1 = H1(s)u1и для sys2y2 = H2(s)u2, то после выполнения команды 8 системы получают выход, равный сумме выходов:
y = H1u1+ H2u2, (12)
а после выполнения команды 9 входы обеих систем объединяются (рис. 7 а, б):
y1 = H1u иy2 = H2u. (13)
Таблица 1. Команды соединения моделей
| № | Команда | Функция |
| append | Объединяет модели в одну | |
| augstate | Расширение выхода добавочными состояниями | |
| connect | Формирует ssмодель с произвольным соединением | |
| feedback | Формирует систему с обратной связью из двух моделей | |
| lft | Производит перекрестное соединение двух моделей | |
| parallel | Параллельное соединение двух моделей | |
| series | Последовательное соединение двух моделей | |
| [ , ] | Каскадное соединение горизонтальное | |
| [ ; ] | Каскадное соединение вертикальное |
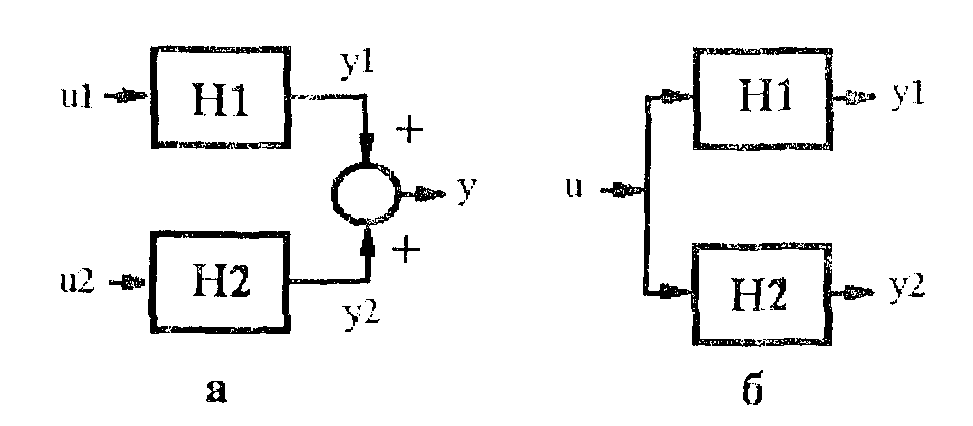
Рис. 7. Каскадное соединение подсистем: а – горизонтальное, б – вертикальное
Пусть, например, мы хотим исследовать влияние коэффициента демпфирования е на переходный процесс в системе второго порядка при толчке на входе при е =0.2 … 1 с шагом 0.2. Создадим 5 систем командами
sys1 = tf(1,[1 2*0.2 1]), sys2 = tf(1,[1 2*0.4 1]), …
с заданными значениями коэффициента демпфирования. Далее выполним команды
sys = [sys1; sys2; sys3; sys4; sys5]
step(sys).(П. 6)
В результате получим график, изображенный на рис. 8.
Командаappend объединяет несколько систем в одну, позволяя оперировать с ними как с одной системой. При выполнении этой команды образуются блочно-диагональные матрицы состояний или передаточных функций, причем эти блоки соответствуют отдельным подсистемам, входящим в объединенную систему. Между собой блоки не связаны. Команда имеет синтаксис:
sys = append(sys1,sys2,…).
Рис. 8. Процессы в системе, образованной каскадным
вертикальным соединением
Числовходящихсистем не ограничено, они должны быть или все непрерывные, или все дискретные с одним и тем же временем выборки. Они могут быть разных типов(FRD, SS, TF, ZPK), причем тип получающейся при этом системы определяется правилом приоритетов:
FRD>SS>ZPK>TF. (14)
Это означаем, что если при соединении ряда моделей хотя бы однаизних есть типа FRD, то и результирующая модель будет этого типа, если такой модели нет, но имеется хотя бы одна модель типа SS, то результирующая модель будет этого типа и т. д. Это же относится и к другим командам.
Если, например, для описанных выше 5-ти систем второго порядка выполнить команду
sys = append(sys1, sys2, sys3, sys4, sys5), (П. 6.1)
то получим передаточную матрицу 5*5, на диагонали которой находятся передаточные функции
1/(s2 + 2e(i)s + 1), e(i) = 0.2*i,
а остальные элементы нулевые.
Командаseriesосуществляет последовательное соединение двух систем. Ее синтаксис
sys= series(sys1, sys2)
или
sys= series(sys1, sys2, outputs1, inputs2).
В первомслучае этакоманда равносильна умножению систем:sys=sys1*sys2. Paзмерности выхода первой системы и входа второй должны быть одинаковы.
Вторая команда реализует более общий случай, когда часть выходов первой системы и часть входов второй могу быть задействованы отдельно (рис. 9). Тогда outputs1– векторномеров (индексов) выходов первой системы, которые должны быть подсосдинены к номерам (индексам) входов второй системы, указанным векторе inputs2(например, outputs1= [1 2], inputs2 =[1 3], если выходы 1 и 2 первой системы должны быть соединены со входами 1 и 3второй системы). Размерности обоих векторов должны быть одинаковы.
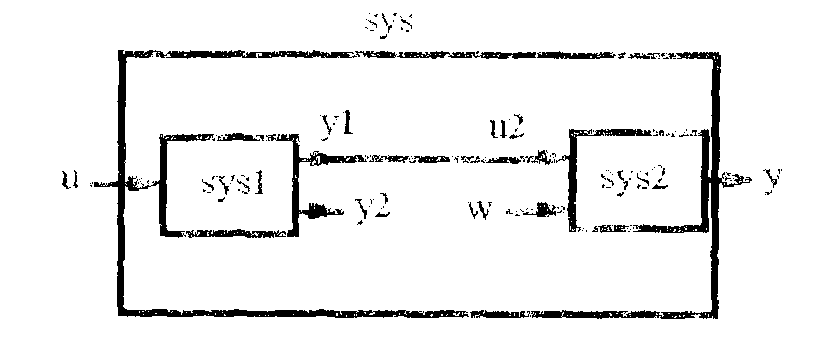
Рис. 9. Команда series
Команда parallelосуществляет параллельное соединение двух cистем. Ее синтаксис
sys = parallel(sysl, sys2)
или
sys = parallel(sysl, sys2, inp1, inp2, out1, out2).
В первом случаеэта команда равносильна сложению систем:sys =sys1 + sys2, входы систем соединяются между собой и наних подаются одинаковые сигналы, а выходы суммируются. Во втором случаеinp1, inp2– векторы, содержащие индексы входовпервой ивторойсистем, соединяемых между собой, aout1,out2 –векторы, содержащие индексы выходов, которые суммируются друг с другом (рис. 10). Пусть, например, каждая система имеет по три входа и по четыре выхода, и мы хотим, чтобы на вход 1 первой системы и вход 2 второй подавался один и тот же сигнал, и то же самое относительно входов 2 и 3. Далее мы хотим, чтобы первые выходы систем суммировались друг с другом, и то же самое относительно вторых входов. Тогда команда запишется так:
sys=parallel(sys1, sys2, [1 2], [2 3], [1 2], [1 2]).
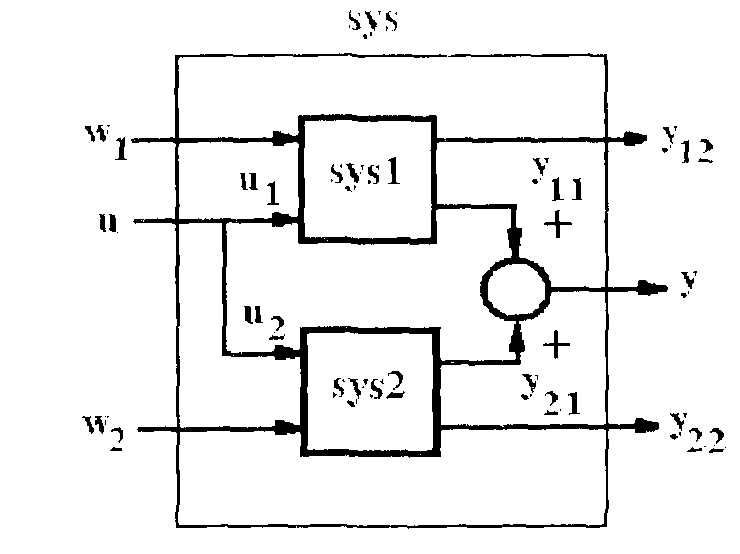
Рис. 10. Команда parallel
При построении системы важное значение имеет команда feedback. По команде, общий вид которой
sys= feedback(sys1, sys2, feedin, feedout, sign),
строится система с syslв прямой связи и sys2 в обратной, причем знак обратной связи +1 или -1 определяется полемsign.Без указания знака система имеет отрицательную образную связь (рис. 11).
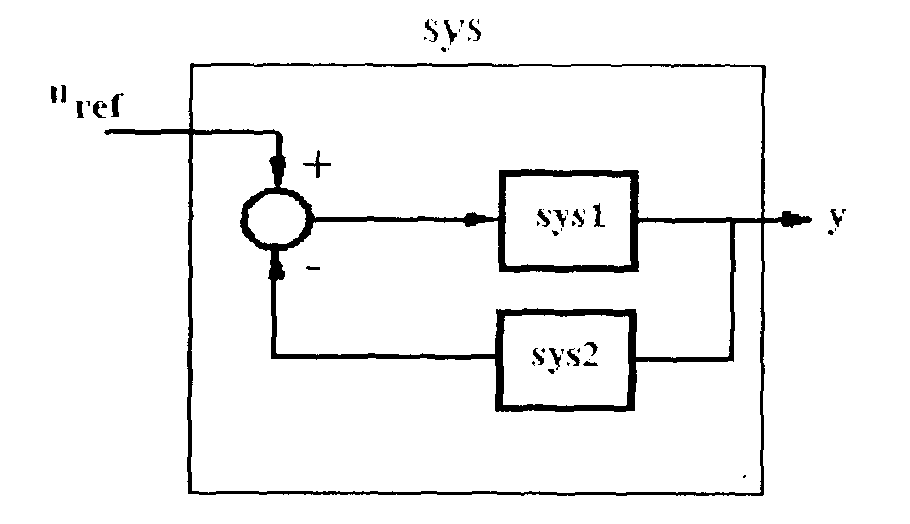
Рис. 11. Команда feedback
Обе системы должны быть либо непрерывные, либо дискретные с одинаковыми периодами квантования. Третье и четвертое поля команды используются в тех случаях, когда на регулятор подается только часть выходов первой системы, и для управления (выход регулятора) также используетсятолько часть входов объекта. Тогдаfeedout–векторномеров (индексов) выходов объекта иfeedin–вектор индексов входа объекта, участвующих в организации обратной связи. Размерностьэтих вектаров должна быть равна размерностям входа и выходарегулятора соответственно.
Пример. Пусть скорость вращении первой инерционной массы в системе, описываемой уравнениями (1.3)...(1.5), должна регулироваться интегро-пропорциональным регулятором с передаточной функцией
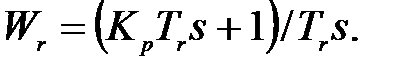 (15)
(15)
Создадим файл (П. 7). Вначале создадим систему 1:
J1 = 21.5; J2 = 7; С = 243;
sys1 = tf([J2 0С], [J1*J2 0C*(J1+J2) 0]). (П.7)
Затем сформируем регулятор:
Tr = 1/350; Кр= 156;
sys2 = tf([Kp*Tr1],[Тг 0]).(П.7.1)
Теперь соединим обе системы последовательно:
sys3 = series(sys2, sys1). (П.7.2)
Для создания замкнутой системы можно поступить двояким образом: или создать систему в обратной связи с коэффицитентом1: sysf = tf(1),а затем применить команду
sys4а = feedback(sys3, sysf). (П.7.3)
или просто написать
sys4b = feedback(sys3, 1). (П.7.4)
Результат в обоих случаях будет одинаков: будет получена передаточная функция замкнутой системы в виде:
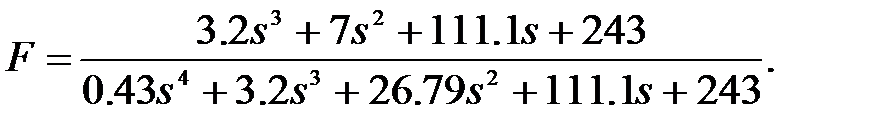 (16)
(16)
Задание. Получите реакцию системы на единичный скачок, вычисленная командой step(sys4a).
На рис. 12 приведена реакция системы на единичный скачок, вычисленная командой step(sys4a).
Рис. 12. Переходной процесс в системе с эластичной муфтой
и ПИ регулятором
Пусть теперь для уменьшения перерегулирования регулятор выполняется чисто интегральным с подчиненным пропорциональным регулятором (рис. 13). Такая система реализуется командами:
sys5=feedback(sys1, Kp)
sys2a=tf(1, [Tr, 0])
sys6=series(sys2a, sys5)
sys7=feedback(sys6,1)
step(sys7). (П.7.5)
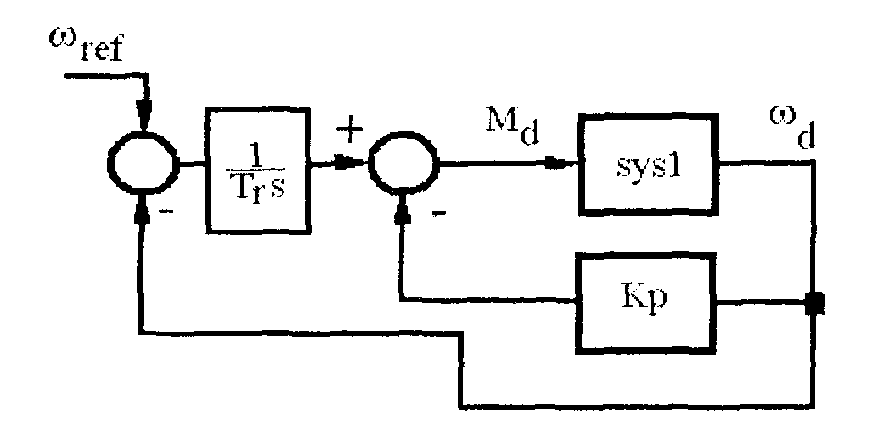
Рис. 13. Cистемaс И регулятороми подчиненным контуром скорости
Передаточная функция системы sys7 получается в виде
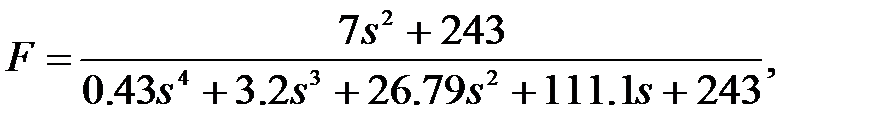 (17)
(17)
а переходный процесс при единичном скачке задания приведен на рис. 14.
Рис. 14. Переходной процесс в системе с И регулятором
и подчиненным контуром скорости
Рассмотрим остальные команды. Команда
sys= lft(sysl, sys2, n, m)
образует перекрестное соединение двух моделейкакна рис. 15. Петля обратной связи соединяет первые n выходов sys2 с последними п входами syslи последниеmвыходов syslс первымиmвходами sys2. Если же п,mне указаны, то получается однаиз двух систем, приведенных на рис. 16, в зависимости от того, какая из систем имеет большее число входов и выходов. Если это первая система, то получается система рис. 16а. а если вторая, то формируется система рис. 16б.
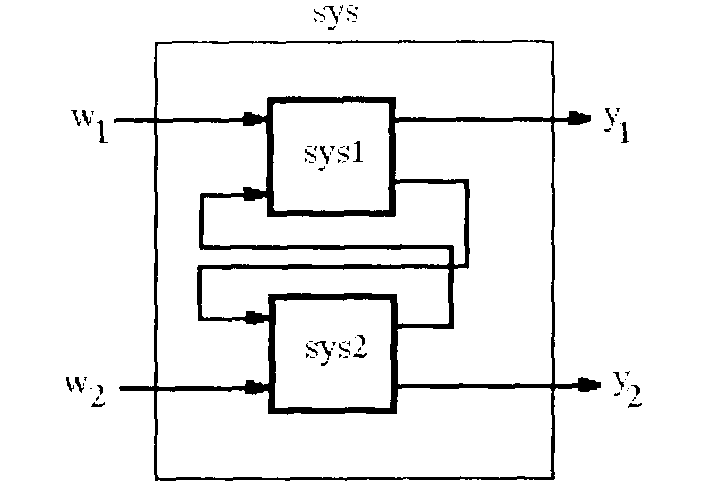
Рис. 15. Команда lft (простой случай)
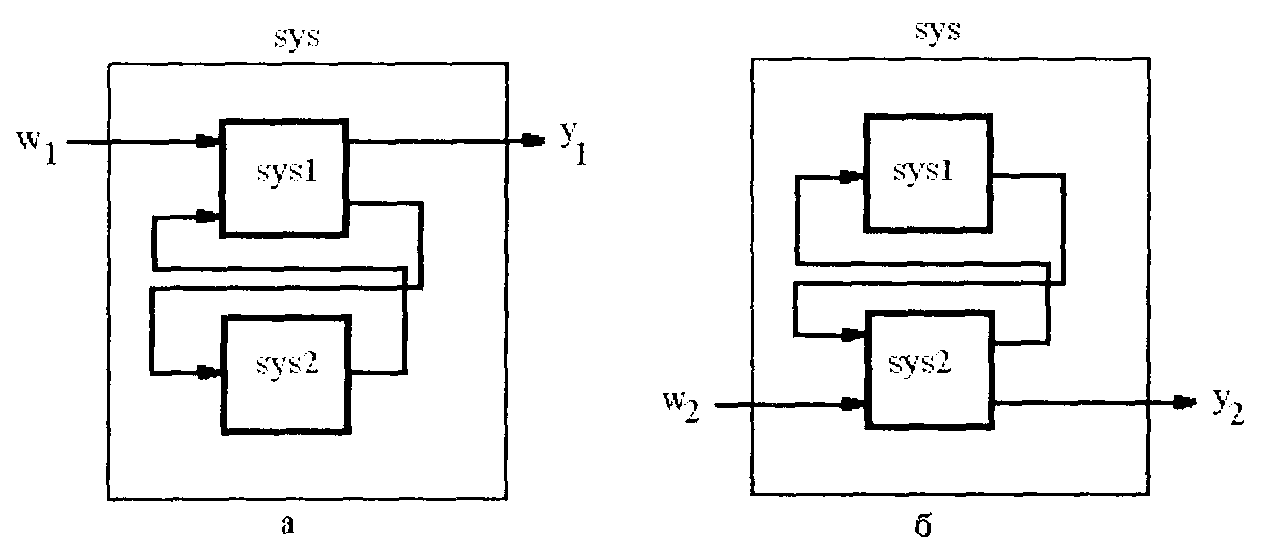
Рис. 16. Команда lft (сложный случай):
а – размерность второй системы меньше первой,
б – размерность второй системы больше первой
Команда augstateрасширяет выход системы, добавляя к у фазовые координаты х, т. е. выход становится равным
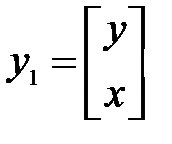 . (18)
. (18)
Эта команда может быть применена как предшествующая замыканию системы по полному состоянию с матрицей обратной связиK(u = -Kx) с использованием командыfeedback.Команда применима только к виду системы SS.
| <== предыдущая страница | | | следующая страница ==> |
| Основные виды обеспечения ЕАИС ТО | | | Командаconnectимеет формат |
Дата добавления: 2014-11-20; просмотров: 333; Нарушение авторских прав

Мы поможем в написании ваших работ!