Расчет надежности систем с последовательным соединением элементов

Существуют структурные схемы надежности системы с последовательным соединением элементов (рис. 11.1), когда отказ одного элемента вызывает отказ другого элемента, а затем третьего и т.д. Например, большинство приводов машин и механизмы передач подчиняются этому условию. Так, если в приводе машины выйдет из строя любая шестерня, подшипник, муфта, рычаг управления, электродвигатель, насос смазки, то весь привод перестанет функционировать. При этом отдельные элементы в этом приводе не обязательно должны быть соединены последовательно.

Такую структурную схему называют схемой с последовательным соединением зависимых элементов. В этом случае надежность системы определяют по теореме умножения для зависимых событий.

Рассмотрим систему, состоящую из двух или более элементов. Пусть А – событие, состоящее в том, что система работает безотказно. a А_i (і = 1,2,..., п)– события, состоящие в исправной работе всех ее элементов. Далее предположим, что событие А имеет место тогда и только тогда, когда имеют место все события А_i, т.е. система исправна тогда и только тогда, когда исправны все ее элементы. В этом случае систему называют последовательной системой.

Рис. 11.1. Структурная схема надежности системы с последовательным соединением элементов

Известно, что отказ любого элемента такой системы приводят, как правило, к отказу системы. Поэтому вероятность безотказной работы системы определяют как произведение вероятностей для независимых событий.

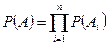. (11.1)

Обозначив Р(А) = Р; Р(А_i) = р_i , получим

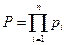, (11.2)

где Р – надежность.

При одинаковой надежности элементов формула (11.2) вероятностей безотказной работы примет вид:

Р(t) = Pⁿ_i.

Сложные системы, состоящие из элементов высокой надежности, могут обладать низкой надежностью за счет наличия большого числа элементов. Например, если узел состоит всего из 50 деталей, а вероятность безотказной работы каждой детали за выбранный промежуток времени составляет Р_i = 0,99, то вероятность безотказной работы узла будет Р(t) = (0,99)⁵⁰ = 0,55.

Если же узел с аналогичной безотказностью элементов состоит из 400 деталей, то Р(t) = (0,99)⁴⁰⁰ = 0,018, т.е. узел становится практически неработоспособным.

Пример 11.1. Определить надежность автомобиля (системы) при движении на заданное расстояние, если известны надежности следующих подсистем: системы зажигания р₁ = 0,99; системы питания топливом и смазкой p₂ = 0,999; системы охлаждения p₃ = 0,998; двигателя p₄ = 0,985; ходовой части p₅ = 0,997.

Решение. Известно, что отказ любой подсистемы приводит к отказу автомобиля. Для определения надежности автомобиля используем формулу (11.2)

Р = р₁ р₂ р₃ р₄ р₅ = 0,990,9990,9980,9850,997 = 0,979.

Если причина выхода из строя деталей машин или узла связана только с внезапными отказами, которые подчиняются экспоненциальному закону, то

; , …

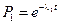то вероятность безотказной работы также подчиняется экспоненциальному закону

,

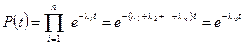где .

Дата добавления: 2014-11-20; просмотров: 846; Нарушение авторских прав

Мы поможем в написании ваших работ!