
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Основы логики. Таблицы истинности. Логические законы и правила преобразования логических выражений. Логические схемы
Высказывание – это повествовательное утверждение, про которое можно однозначно сказать, что оно истинно или оно ложно. Эти два значения всевозможных высказываний обозначаются «истина» и «ложь» или «true» и «false» или «1» и «0». Переменная, значениями которой могут быть лишь значения «1» и «0» называется логической переменной или булевой переменной.
Предикат – выражение с логическими переменными.
Пример. Определить значения следующих высказываний,
«Треугольник – это геометрическая фигура» – истинное высказывание,
«Париж – столица Китая» – ложное высказывание,
«X>7» – предикат,
«Ясная погода» – не является высказыванием,
«Сегодня ясная погода и я пойду в парк» – сложное высказывание.
Логической функцией - называется функция, у которой аргумент – логическая переменная, а значения функции из множества {0,1}.
Конъюнкция (логическое умножение). В русском языке она выражается союзом «И». В математической логике используются знаки & или 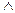 . Конъюнкция – двухместная операция; записывается в виде: А
. Конъюнкция – двухместная операция; записывается в виде: А 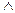 В. Значение такого выражения будет ЛОЖЬ, если хотя бы значение одного из операндов ложно:
В. Значение такого выражения будет ЛОЖЬ, если хотя бы значение одного из операндов ложно:
| Х | Y | X И Y (А 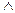 В) В)
|
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |

Дизъюнкция (логическое сложение). В русском языке этой связке соответствуют союз ИЛИ. В математической логике она обозначается знаком 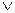 . Дизъюнкция – двухместная операция; записывается в виде: А
. Дизъюнкция – двухместная операция; записывается в виде: А 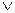 В. Значение такого выражения будет ИСТИНА, если значение хотя бы одного из операндов истинно.
В. Значение такого выражения будет ИСТИНА, если значение хотя бы одного из операндов истинно.
| Х | Y | X ИЛИ Y (А 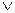 В) В)
|
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |

Инверсия (отрицание). В русском языке этой связке соответствует частица НЕ (в некоторых высказываниях применяется оборот «неверно, что...»). Отрицание – унарная (одноместная) операция; записывается в виде:  А или
А или  .
.
| Х | Не Х (  ). ).
|
| И | Л |
| Л | И |
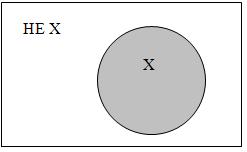
Множество логических переменных с определенными над ним операциями инверсии, конъюнкции, дизъюнкции называется алгеброй предикатов, высказываний.
Таблица всех значений логической функции называется таблицей истинности функции.
Последовательность выполнения операций в логических формулах определяется старшинством операций. В порядке убывания старшинства, логические операции расположены так: отрицание, конъюнкция, дизъюнкция. Кроме того, на порядок операции влияют скобки, которые можно использовать в логических формулах.
Указанные операции удовлетворяют аксиомам:
1. Аксиома инволюции (двойного отрицания): 
2. Аксиомы де Моргана: 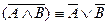 ;
; 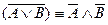
3. Аксиомы поглощения:  ,
, 
4. Аксиомы коммутативности (переместительный закон)
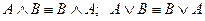
5. Аксиомы ассоциативности (сочетательный закон)

6. Аксиомы идемпотентности
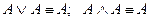
7. Аксиомы дистрибутивности (распределительный закон)
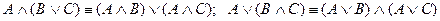
8. Аксиома склеивания
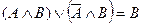 ;
; 
Из этих аксиом следует ряд соотношений:
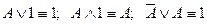
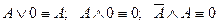
Для описания функционирования аппаратных средств компьютера используется аппарат алгебры логики. Он удобен т.к. основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, и значений логических переменных тоже два: “1” и “0”. Одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных. На этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч операций которых состоят основные узлы компьютера.
Логические функции реализуются технически с помощью трех базовых простых логических элементов (вентилей) т.е. электронных схем И, ИЛИ, НЕ и их комбинаций т.е. И-НЕ, ИЛИ-НЕ и другие. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера.
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Логические функции «инверсия», «дизъюнкция» и «конъюнкция» реализуются элементами ЭВМ (логическими схемами) называемыми соответственно инвертор, дизъюнктор и конъюнктор. Схематически инвертор, дизъюнктор и конъюнктор на схемах различных логических функций можно изобразить следующим образом:
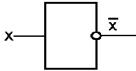

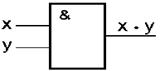
Из этих трех базовых простых логических элементов собираются, конструируются сложные логические схемы ЭВМ: сумматоры, шифраторы, дешифраторы и др.
Вопросы для самоконтроля
1. Что такое высказывание, предикат, логическая функция? Приведите примеры.
2. Каковы аксиомы алгебры логики?
3. Каковы основные три операции алгебры логики?
4. Что такое логическая схема, для чего она применяется?
5. Каковы базовые вентили? Нарисуйте их схемы.
| <== предыдущая страница | | | следующая страница ==> |
| Задачи и упражнения. 1.Перевести заданные целые десятичные числа в двоичную, восьмеричную и шестнадцатеричную системы счисления (до четвертого знака после запятой) и сделать | | | Задачи и упражнения |
Дата добавления: 2014-11-24; просмотров: 940; Нарушение авторских прав

Мы поможем в написании ваших работ!