Задачи и упражнения

1. Какие из предложений являются высказываниями? Определите их истинность.

а) Не все простые числа нечетные.

b) Принеси мне, пожалуйста, книгу!

c) Все студенты любят математику.

2. Определите значение истинности следующих высказываний:

а) Буква «а» – первая буква в слове «аист» или «сова».

б) Две прямые на плоскости параллельны или пересекаются.

с) (13-2∙7) ∙4 = 4.

3. Определить множество истинности предиката р на множестве X:

а) р(х) = 5x<32, x Х=(-∞;∞);

б) р(х)= «х четное число», х Х=[3;15];

4. Упростить логическое выражение z, затем построить таблицу истинности и указать хотя бы одну функцию, эквивалентную данной:

а) z=

б) z=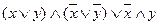

с) z=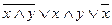

д) z=

е) z=

ж) z=

з) y=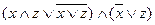

к) z=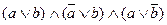

л) z=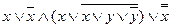

м)

5. Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая находку, каждый высказал по 2 предположения:

Алеша: «Это сосуд греческий и изготовлен в V веке».

Борис: «Это сосуд финикийский и изготовлен в III веке».

Гриша: « Это сосуд не греческий и изготовлен в IV веке».

Учитель истории сказал ребятам, что каждый из них прав в одном из двух предположений. Где и в каком веке изготовлен сосуд?

6. Познакомимся с группой строителей. Их пять человек: Андреев, Борисов, Иванов, Петров и Сидоров. Профессии у них разные: один из них – маляр, другой – плотник, третий – штукатур, четвертый – каменщик, пятый – электрик. Они рассказали о себе следующее. Петров и Иванов никогда не держали в руках малярной кисти. Петров и Борисов живут в одном доме со штукатуром. Андреев и Петров подарили электрику красивую вазу. Борисов и Петров помогали плотнику строить гараж. Сидоров и Борисов по субботам встречаются у электрика, а штукатур по воскресеньям приходит в гости к Андрееву. Определите по этим данным у кого какая профессия.

7.Туристическая фирма наняла на работу трех переводчиков: Иванова, Петрова и Сидорова знающих: французский, итальянский, испанский, немецкий, английский, японский языки. По небрежности отдела кадров при приеме на работу не было указано кто из переводчиков каким языком владеет. Из наблюдений сотрудников фирмы стало известно, что Петров самый молодой из переводчиков. Переводчик с французского старше переводчика с итальянского. Все трое – переводчик с французского, переводчик с итальянского и Иванов – любят играть в теннис. Когда между переводчиком с испанского и переводчиком с японского возникает спор, Петров помогает разрешить его. Иванов признался, что не знает ни японского, ни английского языка. Определите какими языками владеет каждый из переводчиков, если каждый переводчик знает по два различных языка.

8. Брауну, Джонсу, Смиту предъявлено обвинение в соучастии в ограблении банка. Служители банка показали, что похитители скрылись на автомобиле. Браун на суде подтвердил, что похитители скрылись на синем бьюике. Джонсон сказал, что это был черный Крайслер. Смит же утверждал, что это был форд-мустанг и не в коем случае не синий. Стало известно, что, желая запутать следствие, каждый из них указал правильно либо марку, либо цвет автомобиля. Какой марки и какого цвета был разыскиваемый автомобиль?

9. В выпускных классах школы 77 учеников. Из них Биологией увлекается 32, Информатикой – 35, Физикой – 37, Биологией и Информатикой – 13, Биологией и Физикой – 11, Информатикой и Физикой – 11, Биологией, Информатикой и Физикой – 6 учеников. Сколько человек ничем не увлекается?

10. Построить логические схемы, соответствующие функциям:

а)

б)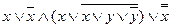

с)

11. Определить логическую функцию, реализуемую следующей схемой:

Задачи и упражнения для самостоятельного решения

1. Какие из предложений являются высказываниями? Определите их истинность.

а) У каждой лошади есть хвост.

в) Я купил велосипед!

с) Вы были в театре?

d) Некоторые люди имеют голубые глаза.

2. Определите значение истинности следующих высказываний:

a) Сумма двух нечетных чисел есть нечетное число.

b) Частное от деления числа 7 на нуль равно 0.

c) Родственные слова имеют общую часть, и они сходны по смыслу.

3. Определить множество истинности предиката р на множестве X:

а) р(х) = 3x-2< -11, x Х(-∞;∞);

б) р(х)= «х нечетное число» , х Х=[1;8];

с) р(х,у)= «число х является делителем числа у» , х,у Х=[3;6], x,y – целые;

4. В соревнованиях по гимнастике участвуют Алла, Валя, Сима и Даша. Болельщики высказали предположения о возможных победителях:

первой будет Сима, Валя будет второй;

второй будет Сима, Даша – третьей;

Алла будет второй, Даша – четвертой.

По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое ложно. Какое место на соревнованиях заняла каждая из девушек, если все они оказались на разных местах.

5. Даны 10 мешков, набитых монетами. Известно, что все монеты в 9 мешках не фальшивые. Относительно же одного мешка известно, что в нем либо все монеты фальшивые, либо все настоящие. Фальшивая монета весит 11 грамм, а настоящая – 10 грамм. Описать способ определения (если он есть) мешка с фальшивыми монетами с помощью одного взвешивания.

6. Является ли самый высокий парень среди студентов самым высоким студентом среди парней?

7. Подобрать три функции, эквивалентные данной функции, но более простого вида (с меньшим числом операций и операндов):

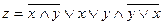
8. Упростить логическое выражение z, затем построить таблицу истинности и указать хотя бы одну функцию, эквивалентную данной:

a) ;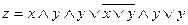

b) ;

c) .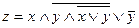

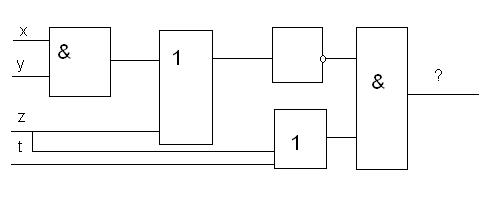
9. Определить логическую функцию, реализуемую следующей схемой:

Дата добавления: 2014-11-24; просмотров: 886; Нарушение авторских прав

Мы поможем в написании ваших работ!