Используемые формулы

1. Вычисление расстояния между двумя точками с координатами (x₁, y₁) и (x₂, y₂), расположенными на плоскости: .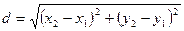

2. Определение расстояния от точки (x₁, y₁) до прямой Ax+By+C=0: .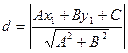

Варианты заданий

1. Требуется разработать класс «Треугольник», при условии, что треугольник задан на плоскости координатами своих вершин. В классе предусмотреть описание следующих свойств треугольника: длина стороны; высота; периметр. С использованием класса вычислить площадь треугольника. Предусмотреть три варианта (разное основание) вычисления. Для вычисления высот треугольника воспользоваться формулами:

; .

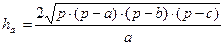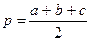Рекомендации:

a. Класс «Треугольник» должен иметь конструктор с шестью параметрами — координатами вершин.

b. Свойства: длина стороны, периметр, высота должны быть доступны только для чтения.

c. Свойства ‘длина стороны’ и ‘высота’ должны быть индексированными.

d. Вычисление площади реализовать в виде метода с параметром — номер стороны.

e. Дополнительно. Реализовать индексированное свойство ‘площадь’.

2. Требуется разработать класс «Треугольник», при условии, что треугольник задан на плоскости длинами своих сторон. В классе предусмотреть описание следующих свойств треугольника: длина стороны; высота; периметр. С использованием класса вычислить площадь треугольника. Предусмотреть три варианта (разное основание) вычисления. Для вычисления высот треугольника воспользоваться формулами:

; .

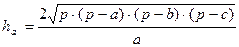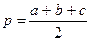Рекомендации:

a. Класс «Треугольник» должен иметь конструктор с тремя параметрами — длинами сторон.

b. Свойства периметр, высота должны быть доступны только для чтения.

c. Свойство ‘длина стороны’ должно допускать и чтение и запись.

d. Свойства ‘длина стороны’ и ‘высота’ должны быть индексированными.

e. Вычисление площади реализовать в виде метода с параметром — номер стороны.

f. Дополнительно. Реализовать индексированное свойство ‘площадь’.

3. Требуется разработать класс «Треугольник», при условии, что треугольник задан на плоскости координатами своих вершин. В классе предусмотреть описание следующих свойств треугольника: длина стороны; медиана. С использованием класса вычислить все медианы треугольника и найти наибольшую из них. Для вычисления медиан треугольника воспользоваться формулой вида: .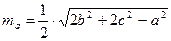

Рекомендации:

a. Класс «Треугольник» должен иметь конструктор с шестью параметрами — координатами вершин.

b. Свойства длина стороны, медиана должны быть доступны только для чтения.

c. Свойства ‘длина стороны’ и ‘медиана’ должны быть индексированными.

d. Поиск наибольшей медианы реализовать в виде метода.

e. Дополнительно. Реализовать индексированное свойство ‘площадь’.

4. Требуется разработать класс «Трапеция», при условии, что трапеция задана на плоскости координатами своих вершин. В классе предусмотреть описание следующих свойств трапеции: длина стороны; высота; площадь, периметр. С использованием класса вычислить периметр и площадь трапеции. Для вычисления воспользоваться формулами вида: .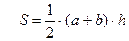

Рекомендации:

a. Класс «Трапеция» должен иметь конструктор с восемью параметрами — координатами вершин.

b. Свойства длина стороны, высота, площадь, периметр должны быть доступны только для чтения.

c. Свойство ‘длина стороны’ должны быть индексированным.

5. Требуется разработать класс «Квадрат», при условии, что квадрат задан на плоскости координатами своих вершин. В классе предусмотреть описание следующих свойств квадрата: длина стороны; периметр; площадь; длина диагонали. С использованием класса вычислить периметр и площадь квадрата.

Рекомендации:

a. Класс «Квадрат» должен иметь конструктор с четырьмя параметрами — координатами двух вершин.

b. Свойства: длина стороны, длина диагонали, площадь, периметр, должны быть доступны только для чтения.

6. Требуется разработать класс «Прямая», при условии, что прямая линия задана на плоскости своими параметрами A, B, C ( 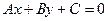). В классе предусмотреть описание следующих свойств прямой линии: угловой коэффициент; отрезок, отсекаемый на оси X; отрезок, отсекаемый на оси Y. С использованием класса вычислить площадь треугольника, ограниченного координатными осями и прямой линией.

Рекомендации:

a. Класс «Прямая» должен иметь конструктор с тремя параметрами — (A, B, C).

b. Свойства: отрезки по осям, угловой коэффициент, должны быть доступны только для чтения.

7. Требуется разработать класс «Треугольник», при условии, что треугольник задан на плоскости координатами своих вершин. В классе предусмотреть описание следующих свойств треугольника: длина стороны; радиус описанной окружности. С использованием класса вычислить разность между длиной описанной окружности и периметром треугольника. Для вычисления радиуса окружности, описанной вокруг треугольника, можно воспользоваться формулами вида: , .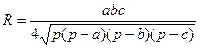

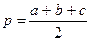Рекомендации:

a. Класс «Треугольник» должен иметь конструктор с шестью параметрами — координатами вершин.

b. Свойства треугольника: длина стороны, периметр, радиус, должны быть доступны только для чтения.

c. Свойство ‘длина стороны’ должны быть индексированным.

8. Требуется разработать класс «Треугольник», при условии, что треугольник задан на плоскости координатами своих вершин. В классе предусмотреть описание следующих свойств треугольника: длина стороны; радиус вписанной окружности. С использованием класса вычислить разность между длиной вписанной окружности и периметром треугольника. Для вычисления радиуса окружности, описанной вокруг треугольника, можно воспользоваться формулами вида: , .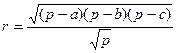

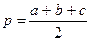Рекомендации:

a. Класс «Треугольник» должен иметь конструктор с шестью параметрами — координатами вершин.

b. Свойства треугольника: длина стороны, периметр, радиус, должны быть доступны только для чтения.

c. Свойство ‘длина стороны’ должны быть индексированным.

9. Требуется разработать класс «Ромб», при условии, что ромб задан на плоскости координатами своих вершин. В классе предусмотреть описание следующих свойств ромба: длина стороны; синус угла; площадь. С использованием класса вычислить отношение периметра ромба к его площади. Для вычисления воспользоваться формулами вида: .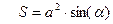

Рекомендации:

a. Класс «Ромб» должен иметь конструктор с восемью параметрами — координатами четырех вершин.

b. Свойства: длина стороны; синус угла, должны быть доступны только для чтения.

c. Свойства ‘длина стороны’ и ‘синус угла’ должны быть индексированным.

10. Требуется разработать класс «Две прямые», если отдельная прямая задана на плоскости своими параметрами: A, B, C ( 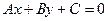). В классе предусмотреть описание следующих свойств: угол между прямыми; отрезок, отсекаемый отдельной прямой на оси X; отрезок, отсекаемый отдельной прямой на оси Y. С использованием класса определить, являются ли две заданные прямые параллельными. Для вычисления угла воспользоваться формулой: .

Рекомендации:

a. Класс «Две прямые» должен иметь конструктор с двумя параметрами типа структуры с (A, B, C).

b. Свойства: угол между прямыми; отрезок, отсекаемый отдельной прямой на оси X; отрезок, отсекаемый отдельной прямой на оси Y — должны быть доступны только для чтения.

c. Свойства ‘отрезок, отсекаемый отдельной прямой на оси’ должны быть индексированными.

d. Вычисление ‘отрезок, отсекаемый отдельной прямой на оси’ реализовать в виде метода с параметром — номер прямой.

11. Требуется разработать класс «Ромб», при условии, что ромб задан на плоскости координатами своих вершин. В классе предусмотреть описание следующих свойств ромба: длина стороны; диагональ меньшая; диагональ большая; площадь. С использованием класса вычислить отношение периметра ромба к его площади. Для вычисления воспользоваться формулами вида: 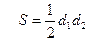, где d1, d2 — диагонали ромба.

Рекомендации:

a. Класс «Ромб» должен иметь конструктор с восемью параметрами — координатами четырех вершин.

b. Свойства: длина стороны; диагональ меньшая; диагональ большая; площадь, должны быть доступны только для чтения.

c. Свойство ‘длина стороны’ должно быть индексированным.

12. Требуется разработать класс «Два трехмерных вектора», предназначенный для выполнения действий над двумя векторами, заданными своими координатами. В классе предусмотреть описание следующих свойств: сумма векторов; разность векторов; скалярное произведение векторов; длина (модуль) вектора. Для вычисления воспользоваться формулами вида: 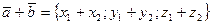. С использованием класса вычислить отношение модулей суммы векторов к модулю разности.

Рекомендации:

a. Класс «Два трехмерных вектора» должен иметь конструктор с двумя параметрами типа структуры с тремя координатами.

b. Свойства: сумма векторов; разность векторов; скалярное произведение векторов; длина вектора — должны быть доступны только для чтения.

13. Требуется разработать класс «Треугольник», при условии, что треугольник задан на плоскости длинами своих сторон. В классе предусмотреть описание следующих свойств треугольника: длина стороны; периметр; высота. С использованием класса вычислить площадь треугольника. Предусмотреть три варианта (разное основание) вычисления. Для вычисления высот треугольника воспользоваться формулами:

; .

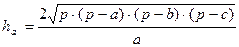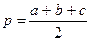Рекомендации:

a. Класс «Треугольник» должен иметь конструктор с тремя параметрами — длинами сторон.

b. Свойства треугольника: длина стороны; периметр; высота, должны быть доступны только для чтения.

c. Свойство ‘высота’ должно быть индексированным.

14. Требуется разработать класс «Треугольник», при условии, что треугольник задан на плоскости координатами своих вершин. В классе предусмотреть описание следующих свойств треугольника: длина стороны; высота; медиана, периметр. С использованием класса вычислить площадь треугольника. Предусмотреть три варианта (разное основание) вычисления. Для вычисления высот треугольника воспользоваться формулами:

; ,

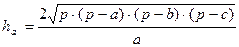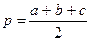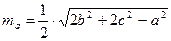
Рекомендации:

a. Класс «Треугольник» должен иметь конструктор с шестью параметрами — координатами вершин.

b. Свойства: длина стороны, периметр, медиана, высота должны быть доступны только для чтения.

c. Свойства ‘длина стороны’, ‘медиана’ и ‘высота’ должны быть индексированными.

d. Вычисление площади реализовать в виде метода с параметром — номер стороны.

e. Дополнительно. Реализовать индексированное свойство ‘площадь’.

15. Требуется разработать класс «Треугольник», при условии, что треугольник задан на плоскости длинами своих сторон. В классе предусмотреть описание следующих свойств треугольника: длина стороны; периметр; биссектриса. С использованием класса вычислить все биссектрисы треугольника и найти наибольшую из них. Для вычисления биссектрис треугольника воспользоваться формулами вида: ; .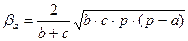

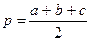Рекомендации:

a. Класс «Треугольник» должен иметь конструктор с тремя параметрами — длинами сторон.

b. Свойства треугольника: длина стороны; периметр; биссектриса, должны быть доступны только для чтения.

c. Свойство ‘биссектриса’ должно быть индексированным.

16. Требуется разработать класс «Треугольник», при условии, что треугольник задан на плоскости длинами своих сторон. В классе предусмотреть описание следующих свойств треугольника: длина стороны; радиус описанной окружности. С использованием класса вычислить разность между длиной описанной окружности и периметром треугольника. Для вычисления радиуса окружности, описанной вокруг треугольника, можно воспользоваться формулами вида: , .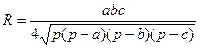

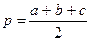Рекомендации:

a. Класс «Треугольник» должен иметь конструктор с тремя параметрами — длинами сторон.

b. Свойства треугольника: длина стороны; радиус, должны быть доступны только для чтения.

c. Свойство ‘длина стороны’ должно быть индексированным.

17. Требуется разработать класс «Квадрат», при условии, что квадрат задан на плоскости координатой левой верхней вершины и длиной стороны. В классе предусмотреть описание следующих свойств квадрата: длина стороны; периметр; площадь; длина диагонали. С использованием класса вычислить периметр и площадь квадрата.

Рекомендации:

a. Класс «Квадрат» должен иметь конструктор с тремя параметрами — координатами одной вершины и длиной стороны.

b. Свойства: длина стороны; периметр; площадь; длина диагонали, должны быть доступны только для чтения.

18. Требуется разработать класс «Треугольник», при условии, что треугольник задан на плоскости длинами своих сторон. В классе предусмотреть описание следующих свойств треугольника: длина стороны; медиана. С использованием класса вычислить все медианы треугольника и найти наибольшую из них. Для вычисления медиан треугольника воспользоваться формулой вида: .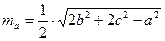

Рекомендации:

a. Класс «Треугольник» должен иметь конструктор с тремя параметрами — длинами сторон.

b. Свойства треугольника: длина стороны; медиана, должны быть доступны только для чтения.

c. Свойство ‘медиана’ должно быть индексированным.

19. Требуется разработать класс «Треугольник», при условии, что треугольник задан на плоскости координатами своих вершин. В классе предусмотреть описание следующих свойств треугольника: длина стороны; периметр; площадь. С использованием класса вычислить площадь треугольника. Для вычисления площади воспользоваться формулой:

.

Рекомендации:

a. Класс «Треугольник» должен иметь конструктор с шестью параметрами — координатами вершин.

b. Свойства: длина стороны; периметр; площадь должны быть доступны только для чтения.

c. Свойства ‘длина стороны’ должны быть индексированными.

d. Вычисление ‘длина стороны’ реализовать в виде метода с параметром — номер стороны.

20. Требуется разработать класс «Прямоугольный параллелепипед», предназначенный для обработки прямоугольных параллелепипедов, если параллелепипед задан длинами сторон. В классе предусмотреть описание следующих свойств: площадь грани; периметр грани, диагональ грани; объем параллелепипеда. С использованием класса необходимо произвести вычисления объема параллелепипеда несколькими способами.

Рекомендации:

a. Класс «Прямоугольный параллелепипед» должен иметь конструктор с тремя параметрами — длинами сторон.

b. Свойства параллелепипед: площадь грани; периметр грани, диагональ грани; объем параллелепипеда — должны быть доступны только для чтения.

21. Требуется разработать класс «Ромб», при условии, что ромб задан на плоскости координатами своих вершин. В классе предусмотреть описание следующих свойств ромба: длина стороны; диагональ меньшая; диагональ большая; площадь. С использованием класса вычислить отношение периметра ромба к его площади. Для вычисления воспользоваться формулами вида: 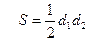, где d1, d2 — диагонали ромба.

Рекомендации:

a. Класс «Ромб» должен иметь конструктор с восемью параметрами — координатами четырех вершин.

b. Свойства: длина стороны; диагональ меньшая; диагональ большая; площадь, должны быть доступны только для чтения.

c. Свойство ‘длина стороны’ должно быть индексированным.

22. Требуется разработать класс «Две прямые», если отдельная прямая задана на плоскости своими параметрами: A, B, C ( 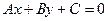). В классе предусмотреть описание следующих свойств: угол между прямыми; отрезок, отсекаемый отдельной прямой на оси X; отрезок, отсекаемый отдельной прямой на оси Y. С использованием класса определить, являются ли две заданные прямые параллельными. Для вычисления угла воспользоваться формулой: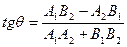

Рекомендации:

c. Класс «Две прямые» должен иметь конструктор с двумя параметрами типа структуры с (A, B, C).

d. Свойства: отрезки по осям, угловой коэффициент, должны быть доступны только для чтения.

e. Свойство ‘Отрезок по оси’ должно быть индексированным.

Дата добавления: 2014-11-24; просмотров: 419; Нарушение авторских прав

Мы поможем в написании ваших работ!