
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Цилиндрические поверхности
Занятие. поверхности ВТОРОГО ПОРЯДКА
Всякая поверхность рассматривается как геометрическое место точек, может быть представлена уравнением относительно координат её точек.
Уравнение поверхности второго порядка имеет вид:
a11x2 + a22y2 + a33z2 + a12xy + a13xz + a23yz + b1x + b2y + b3z + c = 0,
где x, y, z – текущие координаты точки на поверхности.
На данной лекции мы рассмотрим основные поверхности второго порядка.
Объявить тему, цель занятия и литературу.
Цилиндрические поверхности
Краткий опрос по основным понятиям, изложенным в предыдущей лекции:
1. Какое уравнение называется скалярным уравнением плоскости?
2. Какое уравнение называется уравнением плоскости, проходящей через три точки?
3. По какой формуле вычисляется угол между двумя плоскостями?
4. Какие уравнения называются параметрическими уравнениями прямой?
5. Какие уравнения называются уравнениями прямой, проходящей через две точки?
6. По какой формуле вычисляется угол между двумя прямыми?
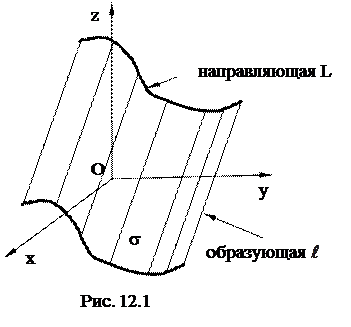 Определение 12.1. Поверхность, составленная из всех прямых, пересекающих данную линию L и параллельных данной прямой
Определение 12.1. Поверхность, составленная из всех прямых, пересекающих данную линию L и параллельных данной прямой 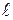 , называется цилиндрической поверхностью. При этом линия L (рис. 12.1) называется направляющей цилиндрической поверхности, а каждая из прямых, составляющих эту поверхность и параллельных прямой
, называется цилиндрической поверхностью. При этом линия L (рис. 12.1) называется направляющей цилиндрической поверхности, а каждая из прямых, составляющих эту поверхность и параллельных прямой 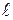 - образующей.
- образующей.
В дальнейшем мы будем рассматривать только такие цилиндрические поверхности, направляющие которых лежат в одной из координатных плоскостей, а образующие параллельны координатной оси, перпендикулярной этой плоскости.
Рассмотрим в плоскости Оxy некоторую линию L (рис.12.2), имеющую в системе координат Оxy уравнение:
F(x, y) = 0. (12.1)
 Построим цилиндрическую поверхность s с образующими, параллельными оси Оz, и направляющей L. Покажем, что уравнение этой поверхности есть уравнение (12.1), если его отнести к системе координат Оxyz в пространстве.
Построим цилиндрическую поверхность s с образующими, параллельными оси Оz, и направляющей L. Покажем, что уравнение этой поверхности есть уравнение (12.1), если его отнести к системе координат Оxyz в пространстве.
Пусть M (x, y, z) – любая фиксированная точка построенной цилиндрической поверхности s. Обозначим через N точку пересечения направляющей L и образующей, проходящей через точку M. Точка N -есть проекция точки M на плоскость Оxy. Поэтому точки M и N имеют одинаковые абсциссу x и ординату y. Но точка N лежит на кривой L, и её координаты x и y удовлетворяют уравнению (12.1) этой кривой. Следовательно, этому уравнению удовлетворяют и координаты точки M(x, y, z), так как оно не содержит z. Таким образом, координаты любой точки M(x, y, z) данной цилиндрической поверхности удовлетворяют уравнению (12.1). Значит, уравнение
F(x, y) = 0 в пространстве является уравнением цилиндрической поверхности с образующими, параллельными оси Оz, и направляющей L, которая в плоскости Оxy задаётся тем же уравнением F (x, y) = 0. В пространстве Оxyz направляющая L определяется системой уравнений
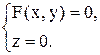
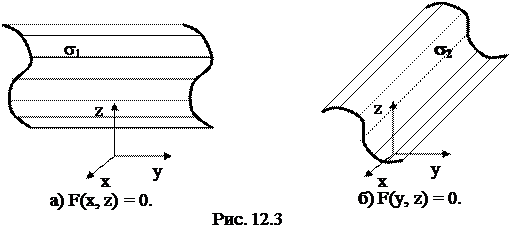 |
Аналогично можно показать, что уравнение F(x, z) = 0, не содержащее y, в пространстве Оxyz определяет цилиндрическую поверхность s1 с образующими, параллельными соответственно оси Оy (рис. 12.3, а).
Точно так же уравнение F(y, z) = 0, не содержащее x, определяет цилиндрическую поверхность s2 с образующими, параллельными оси Ох (рис. 12.3, б).
Таким образом, цилиндрическая поверхность, параллельная какой-либо оси координат, в пространстве может быть задана с помощью уравнения, в аргументах которого отсутствует одна из переменных x, y, z декартовой системы координат. И наоборот, множество точек пространства, координаты которых удовлетворяют "неполному" уравнению (отсутствует одна из переменных), составляет цилиндрическую поверхность, параллельную "отсутствующей переменной".
Вопросы на понимание основных понятий:
1. Какая поверхность называется цилиндрической?
2. Какая линия называется направляющей?
3. Какая прямая называется образующей?
4. Какая переменная «отсутствует» в уравнении цилиндрической поверхности?
| <== предыдущая страница | | | следующая страница ==> |
| БИБЛИОГРАФИЧЕСКИЙ СПИСОК. 2. Цифровая обработка изображений в информационных системах: Учеб | | | Конические поверхности |
Дата добавления: 2014-11-24; просмотров: 441; Нарушение авторских прав

Мы поможем в написании ваших работ!