Цикл Карно. Статистический смысл второго начала термодинамики. Энтропия и вероятность

Карно рассмотрел тепловой двигатель, состоящий из нагревателя с температурой Т₁, холодильника с температурой Т₂ и рабочего тела, т.е. устройства, способного получать тепло и совершать работу. В качестве рабочего тела использовался идеальный газ. Цикл Карно состоял из двух изо­терм и двух адиабат. При изо­термическом расширении 1-2 газ нахо­дится в контакте с нагревателем (Т₁). Пусть при этом газ получает тепло Q₁. На изотерме 3-4 газ отдает тепло Q₂ холодильнику (Т₂). В соответствии с определением КПД двигателя:

.

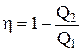Изобразим цикл в системе TS. Полученное тепло и равно площади под отрезком 1–2. Отданное холодильнику тепло и равно площади под отрезком 4–3. Подставив формулы Q₁ и Q₂ в выражение для КПД получим:

.

Теорема Карно: КПД тепловых двигателей, работающих по циклу Карно, зависит только от температуры нагревателя и холодильника и не зависит ни от устройства двигателя, ни от рода вещества.

Соотношение положено в основу термодинамической шкалы температур (Q ~ T). Преимущество этой шкалы заключается в том, что она не зависит от выбора рабочего вещества, используемого для измерения температуры. Для однозначного определения численного значения температуры необходимо условиться о выборе единицы измерения, т.е. градуса. За абсолютный градус принимается одна сотая разности температур кипящей при нормальном атмосферном давлении воды и таяния льда. Таким образом, градус абсолютной термодинамической шкалы равен градусу идеальной газовой шкалы.

Статистический смысл второго начала термодинамики. Энтропия и вероятность.

Состояние системы, которое характеризуется макропараметрами (p,V,T,U…), называется макросостоянием. Состояние макросистемы, при котором заданы состояния всех молекул, называется микросостоянием. Любое макросостояние системы может быть реализовано различными микросостояниями. Статистическим весом макросостояния называется число возможных микросостояний, соответствующих данному макросостоянию. Опыт показывает, что представленная самой себе макросистема стремится переходить от менее вероятным состояниям к более вероятным, при этом вероятность состояния прямо пропорциональна статистическому весу: Р~W. Так как при переходе от менее к более вероятным состояниям возрастает и энтропия, то очевидно предположить, что энтропия пропорциональна статистическому весу. Больцман вывел зависимость между энтропией и статистическим весом:

.

Полученная формула называется формулой Больцмана. Принцип возрастания энтропии привел Больцмана к выводу: все замкнутые макросистемы стремятся переходить от состояний менее вероятных к более вероятным, при этом энтропия характеризует степень беспорядка в макросистеме.

Дальнейшие исследования показали, что статистика Больцмана является приближенной. Более точное описание макросистем можно получить с использованием законов квантовой физики, в которой микропараметры не могут принимать любые значения. Величины, характеризующие микрочастицы, могут принимать только дискретные значения, кратные некоторой const. Согласно квантовой теории все микрочастицы подразделяют на два класса, которым соответствуют две квантовые статисти­ки:

- частицы с полуцелым спином, их называют фермионами; они подчиняются статистике Ферми-Дирака;

- частицы с целым спином – бозоны; они подчиняются статистике Бозе–Эйнштейна.

Во всех статистиках допустимые микросостояния считаются равно­вероятными. Но различие их – в способах определения мик­росостояний и статистических весов. В статистике Больцмана считается, что даже тождественные частицы принципиально различимы. В квантовых же статистиках, наоборот, считается, что тождественные частицы принципиально неразличимы.

В основу статистики Ферми–Дирака положен принцип Паули, согласно которого в каждом квантовом состоянии может находиться не более одной частицы. В статистике Бозе–Эйнштейна в каждом состоянии может находится любое число частиц.

Основная задача квантовых статистик – это нахождение соответствующих им функций распределения частиц по тем или иным параметрам (например, по энергиям), а также определение средних значений этих параметров, ха­рактеризующих наиболее вероятное макросостояние всей сис­темы частиц.

Для описания состояния системы частиц рассматривают во­ображаемое шестимерное пространство, каждая точка которого характеризуется шестью координатами: х, у, z, р_х, р_у, р_z. Это пространство называют фазовым. Состояние системы определяется тем, как распределены в этом пространстве точ­ки, изображающие состояния всех N частиц системы. При этом нужно учесть присущий частицам корпускулярно–волновой ду­ализм, согласно которому неопределенности координаты х и со­ответствующей проекции импульса р_х могут быть определены только с неопределенностью и , произведение которых, согласно принципу неопределенностей Гейзенберга, , где h – постоянная Планка. Данному состоянию части­цы в фазовом пространстве соответствует не точка, а фазовая ячейка, объем которой

Квантовые распределения представля­ют собой функции , определяющие средние числа частиц в одной фазовой ячейке с энергией . Для фермионов:

.

Для бозонов:

где m – химический потенциал, который определяется как некоторая характерная энергия, значение которой можно найти из усло­вия нормировки: суммарное число частиц во всех фазовых ячейках должно быть равно полному числу N частиц макроси­стемы.

Особенности распределений:

- для фермионов функция не может быть больше еди­ницы, а для бозонов ее значение может быть любым;

- если , то в знаменателях обоих распределений можно пренебречь единицей, и формула принимает вид:

,

т. е. получаем распределение Больцмана (А — нормировочный коэффи­циент). Значит, классическое распределение Больцмана спра­ведливо лишь тогда, когда малы «числа заполнения» фазовых ячеек;

- в макросистеме уровни энергии частиц квазинепрерыв­ны (расположены очень плотно);

- для бозонов значения m не могут быть положитель­ными, иначе при окажется, что f < 0, а это лишено физи­ческого смысла. Для фермионов подобного ограничения не существует.

Определим число dZ фазовых ячеек в интервале энергий (Е, Е + dЕ). Для этого найдем сначала соответствующий объем dL фазового шестимерного пространства. Выделим в им­пульсной части фазового пространства шаровой слой радиусом, равным импульсу р частицы, и толщиной dp. Его объем равен 4pp²dp. Умножив его на объем V координатной части фазового пространства, получим искомый элемент объема dL фазового пространства:

.

Число dZ фазовых ячеек в этом элементе объема получим, разделив dL на объем одной фазовой ячейки h³:

.

Зная число dZ фазовых ячеек в ин­тервале энергий (E, E + dE), и среднее число частиц в каждой ячейке, т. е. функцию заполнения f, мы можем найти число частиц dn в данном интервале энергий:

,

где g – числовой коэффициент порядка единицы, связанный со спецификой частиц идеального газа.

Дата добавления: 2014-11-24; просмотров: 459; Нарушение авторских прав

Мы поможем в написании ваших работ!