
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Построение математических моделей ГПС, их устройств и элементов
В ГПС используют блочно-иерархический метод построения моделей, в которой используется трехуровневая или четырехуровневая структура.
Верхний уровень – система взаимодействующих устройств: Технологического оборудования (ТО), ПР, складов, контрольно-измерительных автоматов, автоматического транспорта и др.
Определяется: производительность ГПС, коэффициенты загрузки станков, максимальное и минимальное время обработки и т. д.
ММ на этом уровне может быть описана в виде модели систем массового обслуживания (СМО). СМО описывается модельными блоками, представляющими законы распределения времени обработки изделий на них. На этом уровне:
- выбираются технологические технические объекты (ТО) на обработку;
- определяется оптимальная последовательность выполнения обработки ТО.
Решается задача с помощью теории массового обслуживания. Необходимо определять выбор приоритетов при обработке, стоимость времени ожидания ТО (срочность обработки).
Экономические критерии. Ценность ТО характеризуют величиной α. Выбранная последовательность обработки (приоритетов) является оптимальной, если в установившемся режиме работы системы количество полностью обработанных в единицу времени ТО будет максимальным.
∑αiλiυi → max,
где υi – вероятность полной обработки ТО,
λi – входящий поток ТО с одинаковым приоритетом.
На 2-м уровне каждая из единиц оборудования рассматривается как система из взаимодействующих элементов. Например, робот состоит из манипуляторов, приводов, сенсорных датчиков. Разрабатываются ММ устройств.
Третий уровень – изучение функционирования отдельного элемента (манипулятор, …). Условно можно разделить на 4 типа узлов: механические, управляющие, информационно-сенсорные, приводные. Создаются кинематические и динамические модели механических узлов.
В качестве моделей используют системы обыкновенных дифференциальных уравнений, алгебраических и др. уравнений), или их комбинаций. Для механических узлов необходимо учитывать: порядок соединения звеньев в механизме друг с другом, способ соединения (шарнирный, скольжения или вращательный), массу, координаты центров тяжести, тензор инерций.
Для детального отражения процессов, протекающих в отдельных модельных блоках (звена манипулятора,станина станка с ЧПУ, ротор эл. двигателя) на 4-м уровне используются дифуравнения в частных производных.
Для общесистемных моделей на верхнем иерархическом уровне могут использоваться: детерминированные дискретные модели (ДДМ), стохастические модели (СМ) и непрерывно стохастические модели(НСМ).
Детерминированные дискретные модели.Для их построения используют теорию автоматов. Автомат отрабатывает дискретную информацию и меняет свои внутренние состояния в дискреустимые тные автоматного времени (такты времени). На вход подаются воздействия X, а на выходе получают выходные характеристики Y, имеет внутреннее состояние Z. Если множество внутренних состояний конечное, то автомат конечный. Автомат также характеризуется начальным состоянием z0 (z0 Є Z), функцией состояний h(z,x), функцией выходов g(z,x). По способу задания функции выхода g различают автоматы Мили и Мура.
Автомат Мили описывается уравнениями: z(t+1)=h[z(t),x(t)], y(t)=g[z(t),x(t)], t=0,1,2,3…
Автомат Мура определяется только состоянием автомата и не зависит от входного воздействия. Y(t)=g[z(t)], т.е. функция выходов не зависит от входной переменной x(t) или z(t+1)=h[z(t),x(t)], y(t)=g[z(t),x(t-1)], t=0,1,2,3…
Способы описания: табличный, графовый и матричный.
Табличный – таблица переходов и выходов, строки которых соответствуют входным воздействиям автомата, а столбцы его состояниям.
Таблица . Задание автомата Мили
| xi\ zi | z0 | z1 | zk | |
| x1 x2 … xn | h(z0,x1) h(z0,x2) … h(z0,xn) | h(z1,x1) переходы h(z1,x2)=z(t) … h(z1,xn) | … … … … | h(zk,x1) h(zk,x2) … h(zk,xn) |
| x1 x2 … xn | g(z0,x1) g(z0,x2) … g(z0,xn) | g(z1,x1) выхода g(z1,x2)=ys(t) … g(z1,xn) | … … … … | g(zk,x1) g(zk,x2) … g(zk,xn) |
Таблица . Задание автомата Мура
| g(z0)→y1 | g(z1) →y2 | … | g(zk) →ys | |
| xi\ zi | z0 | z1 | zk | |
| x1 x2 … xn | h(z0,x1) h(z0,x2) … h(z0,xn) | h(z1,x1) h(z1,x2) … h(z1,xn) | … … … … | h(zk,x1) h(zk,x2) … h(zk,xn) |
Графовый способ задания - направленный граф, в котором вершины соответствуют состояниям автомата, а набор дуг соответствует переходам автомата из одного состояния в другое.
Матричный – квадратная матрица соединений автомата ||Сi,j||, строки которой соответствуют исходным состояниям, а столбцы - состояниям переходов. Элемент сi,j=xk/ys соответствует переходу из состояния zi в состояние zj при входном воздействии xk и выходной характеристике ys, получаемой при этом переходе. При описании автомата Мура элемент сi,j равен множеству входных воздействий на переходе (zi → zj), а выход описывается вектором выходов Y, где i - компонента которого – выходная характеристика, отмечающая состояние zi.
│y(z0)│ Пример для автомата Мура │─ x1 ─ x2 ─│ │ y1│
Y=│y(z1)│ │─ x2 ─ ─ x1│ │ y2│
│… │ C =│─ x2 ─ ─ x1│ Y= │ y3│
│y(zk)│ │x2 ─ x1 ─ ─│ │ y2│
│x2 ─ x1 ─ ─│ │ y3│
Данные схемы описания автоматов удобны для описания функционирования ГПС, их подсистем и элементов (ПР, станки с ЧПУ, загрузочные устройства, подсистемы сборки, подсистемы контроля, управления и т.д.). для которых характерно наличие дискретных состояний и дискретный характер работы во времени.
Стохастические моделистроят с использованием теории вероятностных (стохастических) автоматов т.к. ГПС проявляют статистически закономерное случайное поведение. Вероятностный автомат – дискретный потактовый преобразователь объектов обработки с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически.
Пусть существует множество G(xi,zs), где элементы входного подмножества xi и выходного стояний zs образуют всевозможные пары. Элемент xi,zs множества G индуцирует закон распределения из F(z,x,y,h,g), элементы которого (z1,y1), ( z1,y2)… (zk,yj-1), (zk,yj); b11, b12… bkj-1, bkj при этом выполняется условие ∑∑ bkj=1, где bkj – вероятности перехода автомата в состояние zk и появления на выходе сигнала yj, если он находился в состоянии zs и на его вход в этот момент времени поступил сигнал xi. Число таких распределений, представленн ых в виде таблиц равно числу элементов множества G. Обозначим множество таких таблиц через В. Тогда Р=(z,x,y,В) называют вероятностным автоматом.
Пусть элементы множества G индуцируют некоторые законы распределения q и r на множествах y и z. Что можно представить соответственно в виде:
элементы из y: y1 y2 y3… yj-1 yj,
q1 q2 q3… qj-1 qj;
элементы из z: z1 z2 z3… zk-1 zk,
r1 r2 r3… rk-1 rk.
При этом ∑ rk.=1 и ∑ qj.=1, где rk. и qj – вероятности перехода р-автомата в состояние zk и появление сигнала yj при условии, что автомат находился в состоянии zs и на его вход поступил сигнал xi. Если для всех k и j имеет место соотношение rk.qj= bkj, то такой автомат называют вероятностным автоматом Мили. Это требование означает выполнения условия независимости распределений для нового состояния р-автомата и его выходного сигнала.
Пусть каждый элемент выходного подмножества y индуцирует распределение вероятностей выходов, имеющих следующий вид:
элементы из y: y1 y2 y3… yk-1 yk,
s1 s2 s3… sT-1 sT.
∑ si.=1, где si. – вероятность появления выходного сигнала yi при условии, что р-автомат находится в состоянии zk. Если для всех k и i имеет место соотношение zksi.= bkj, то такой автомат называют вероятностным автоматом Мура.
Частным случаем р-автомата, задаваемым как Р=(z,x,y,В), является автомат у которого либо переход в новое состояние, либо выходной сигнал определяются детерминировано. Если выходной сигнал определяется детерминировано, то автомат называют у-детерминированным вероятностным автоматом. Задание у-детерминированного р-автомата эквивалентно заданию некоторой дискретной марковской цепи с конечным множеством состояний. Аппарат марковских цепей является основным при использовании р-схем для аналитических расчетов.
Аналогично z –детеминированным вероятностным автоматом называют р-автомат, у которого выбор нового состояния является детерминированным.
Непрерывно стохастические модели -класс математических схем, разработанных в теории массового обслуживания для формализации процессов функционирования систем обслуживания (процессы обработки технологических объектов, сборки, переработки). ГПС характеризуется случайным появлением на обработку, сборку ТО и завершением их в случайные моменты времени, т.е. наблюдается стохастический характер процесса функционирования ГПС. Типовая сложная СУ в целом является гибридной системой. Под гибридными системами понимаются системы, демонстрирующие как непрерывные, так и дискретные аспекты поведения
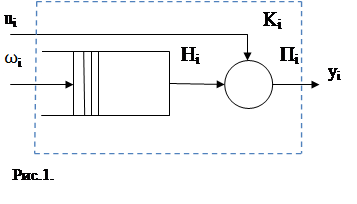
При обслуживании можно выделить две составляющих: ожидание заявок обслуживания и собственно обслуживание заявки. Комплекс по обслуживанию показан на рис.1. и состоит из накопителя заявок Hi в котором может одновременно находится li=0…Li заявок (где Li – емкость i-го накопителя) и выбора обслуживания заявок Пі. На каждый элемент комплекса обслуживания Ki поступают потоки событий: в накопитель Hi поток заявок ωе, на прибор Пі – поток обслуживания ui.
 Интервалы времени между моментами появления заявок на входе Пі образует подмножество неуправляемых переменных, а поток обслуживания ui Є u . интервалы времени между началом и окончанием обслуживания заявки. Образует подмножество управляемых переменных.
Интервалы времени между моментами появления заявок на входе Пі образует подмножество неуправляемых переменных, а поток обслуживания ui Є u . интервалы времени между началом и окончанием обслуживания заявки. Образует подмножество управляемых переменных.
Заявки, обслуженные прибором Пі, и заявки не обслуженные комплексом Ki по разным причинам (например из-за переполнения накопителя Hi), образуют выходной поток yi Є y, т.е. интервалы времени между моментами выхода заявок образуют подмножество выходных переменных.
Процесс функционирования обслуживающего комплекса Ki представляют как процесс изменения состояния его элементов во времени zi(t). Переход в новое состояние Ki означает изменение числа заявок, которые в нем находятся. Вектор состояний для Ki имеет вид zi= (zz) Число заявок в накопителе 0,1… Li , а состояние прибора для обслуживания Пі 0 (свободен) и 1(занят). Оператор сопряжения R, отражает взаимосвязь приборов обслуживания и накопителей (параллельное или последовательное).
Для задания НСМ-схемы необходимо описать алгоритмы ее функционирования, которые определяют набор правил поведения заявок в системе в различных ситуациях. Различают алгоритмы ожидания заявок в накопителе и обслуживания заявок прибором, набор правил, по которым заявки покидают накопитель и прибор обслуживания.
В реальной системе неоднородность заявок учитывается с помощью введения классов приоритетов (статические и динамические). Статические приоритеты назначаются заранее и не зависят от состояний НСМ-схем. Динамические приоритеты зависят от ситуаций.
Правила покидания Hi (переполнения, истечения времени ожидания) и Пі (выбор маршрута или направления ухода) описываются оператором алгоритмов поведения заявок А.Наибольшими возможностями обладают имитационные модели, которые позволяют исследовать НСМ-схему НСМ=(W,U,H,z,Y,R,A) без ограничений.
Имитационное моделирование – это разработка и выполнение на компьютере программной системы, отражающей структуру и функционирование (поведение) моделируемого объекта или явления во времени. Имитационное моделирование имеет преимущество перед аналитическим моделированием в следующих случаях:
- отношения между переменными в модели нелинейные, поэтому аналитические модели невозможно построить;
- модель содержит стохастические компоненты;
- для понимания поведения системы требуется визуализация динамики происходящих в ней процессов;
- модель содержит много параллельно функционирующих взаимодействующих компонентов.
В настоящее время имитационное моделирование насчитывает четыре направления:
- моделирование динамических систем сложных объектов, поведение которых описывается системами алгебро-дифференциальных уравнений ( реализуется в инструментальной среде Simulink)Simulink– интерактивный инструмент для моделирования, имитации и анализа динамических систем. Он дает возможность строить графические блок-диаграммы, имитировать динамические системы, исследовать работоспособность систем и совершенствовать проекты. Simulinkполностью интегрирован с MATLAB, обеспечивая немедленный доступ к широкому спектру инструментов анализа и проектирования.
- дискретно событийное моделирование, в котором потоки пассивных заявок обрабатываются активными приборами (реализована в среде моделирования GPSS, в которой осуществляют моделирование систем массового обслуживания - СМО);
- системная динамика ;
- агентное моделирование.
Можно выделить следующие характерные особенности сложных технических систем []:
- элементы системы имеют разнородные физические принципы действия (электрические, механические, гидравлические, оптические и др. системы);
- между элементами системы, а также с внешней средой имеется множество связей, как информационных, так и физических:
- система имеет иерархическую многоуровневую структуру;
- имеется много различных режимов работы, причем эти режимы не совпадают, то есть, один режим работы одной подсистемы может требовать переключений режимов работы других подсистем;
- имеется значительная неопределенность в поведении объектов управления и внешней среды;
- устройства управления помимо задач обычного непрерывного управления решают также задачи логического управления, диагностики и др.;
- большая часть функций управления реализуется программно на встроенных ЭВМ и микропроцессорах;
- очень часто программное обеспечение и аппаратура разрабатываются одновременно;
часто состав и структура системы изменяется в ходе ее функционирования.

Дата добавления: 2014-11-24; просмотров: 377; Нарушение авторских прав

Мы поможем в написании ваших работ!