Диэлектрики в электрическом поле. Поляризация диэлектриков. Вектор поляризованности. Диэлектрическая проницаемость. Условия на границе раздела диэлектриков

Диэлектриками называ­ют вещества, практически не проводящие электрического тока. Это значит, что в диэлектриках в отличие от про­водников нет зарядов, способных перемещаться на значитель­ные расстояния, создавая ток. Молекулы диэлектриков могут быть полярными и неполярными. У по­лярных молекул центр «тяжести» отрицательного заряда сдви­нут относительно центра тяжести положительных зарядов, в результате чего они обладают собственным дипольным момен­том 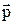. Неполярные молекулы собственным дипольным мо­ментом не обладают: у них центры тяжести положительного и отрицательного зарядов совпадают. Под действием внешнего электрического поля происходит поляризация диэлектрика. Это явление заключает­ся в следующем. Если диэлектрик состоит из неполярных моле­кул, то в пределах каждой молекулы происходит смещение за­рядов – положительных по полю, отрицательных против поля. Если диэлектрик состоит из полярных молекул, то при от­сутствии внешнего поля их дипольные моменты вследствие теплового движения ориентированы хаотически. Под действием внешнего поля дипольные моменты ориентиру­ются преимущественно в направлении внешнего поля. Это приводит к смещению электрических зарядов: положительных по полю, а отрицательных – против поля. В результа­те поляризации на поверхности диэлектрика и в его объеме появляются нескомпенсированные заря­ды, которые называют поляризационными или связанными. Поляризованные заряды могут сме­щаться лишь внутри электрически нейтральных молекул. Заряды, которые не входят в состав молекул диэлектрика, называют сторонними. Эти заряды могут находиться как внутри, так и вне диэлектрика.

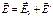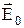Напряженностью поля Е в диэлектрике назы­вается величина, являющаяся суперпозицией поля Е₀ сторонних зарядов и поля Е' связанных зарядов: .где и 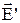представляют собой макрополя, т. е. усредненные по физически бесконечно малому объему микрополя соответствен­но сторонних и связанных зарядов.

Для количественного описания явления поляризации диэлектрика вводят вектр поляризованности 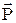, который определяется как дипольный момент единицы объема вещества: 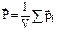,где 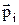– дипольный момент i–го диполя. Пусть в объеме V содержится N диполей концентрация которых определяется из выражения: 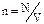. Тогда можно записать:

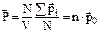,где 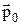– средний дипольный момент одной молекулы.

Единицы поляризованности. Выделим очень малый объем dV внутри диэлектрика. При возникновении поляризации входящий в этот объем поло­жительный заряд 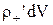сместится относительно отрицательного заряда на величину 1, и эти заряды приобретут дипольный мо­мент 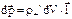. Разделив обе части этого равенства на dV, по­лучим выражение для дипольного момента единицы объема, т.е. вектор поляризованности 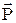: 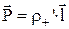. Из полученной формулы следует, что единицей поляризованности в СИ является [Кл/м²].

Связь между векторами напряженности и поляризованности. Опыт показывает, что для большинства диэлектриков поляризованность линейно зависит от напряженности поля: 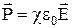, где c – безразмерная величина, которая называется диэлектрической восприимчивостью вещества. Диэлектрическая восприимчивость не зависит от поляризованности а определяется только свойствами диэлектрика.

Свойства поля вектора поляризованности.

Пусть произвольная замкнутая по­верхность S охватывает часть диэлектрика. При включении внешнего электрического поля диэлектрик поля­ризуется – положительные заряды сместятся относите­льно отрицательных. Найдем заряд, который проходит че­рез элемент dS замкнутой поверхности S наружу. Пусть 1₊ и l_– – векторы, характеризующие смещения поло­жительного и отрицательного связанных зарядов в результате поляризации. 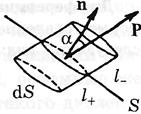Тогда через элемент поверхности dS на­ружу поверхности S выйдет положительный заряд 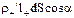, заключенный во внутренней части косого цилиндра. Кроме того, через элемент dS войдет внутрь повер­хности S отрицательный заряд 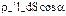, заключенный во внешней части косого цилиндра. Но перенос отрицательного заряда в некотором направлении эквивалентен переносу положительного заряда в противоположном направлении, вследствие чего суммарный связанный за­ряд, выходящий наружу поверхности S через элемент dS, равен: 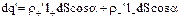.Учитывая, что 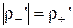, окончательно получаем:

,

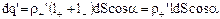где 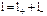– расстояние, на которое сместились относитель­но друг друга положительные и отрицательные связанные за­ряды диэлектрика при поляризации. Учитывая, что 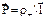, после соответствующей замены получаем: 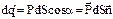.Проинтегрировав это выражение по всей замкнутой поверх­ности S, мы найдем весь заряд, который вышел при поляриза­ции из объема, охватываемого поверхностью S. В результате внутри поверхности S останется некоторый избыточный связанный заряд q’. Ясно, что вышедший заряд должен быть равен с обратным знаком оставшемуся внутри поверхно­сти S избыточному связанному заряду, т.е.:

.

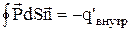Полученное уравнение выражает теорему Гаусса для вектора поляризованности: поток вектора 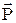сквозь про­извольную замкнутую поверхность S равен взятому с обратным знаком избыточному связанному заряду диэлектрика в объеме, охватываемом поверхностью S.В дифференциальной форме полученное уравнение имеет вид: ,

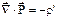т.е. дивергенция поля вектора 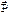равна с обратным знаком объемной плотности избыточного связанного заряда в той же точке.

Так как в общем случае источ­никами поля Е являются все электрические заряды – сторонние и связанные, то теорема Гаусса для поля Е принимает вид: 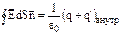или 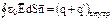где q и q’ – сторонние и связанные заряды, охватывае­мые поверхностью S. Но так как 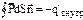, то после соответствующей замены получаем: .

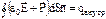Введем вспомогательный вектор 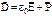– электрическое смещение. Теорема Гаусса для вектора электрического смещения имеет вид: 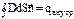.Поток вектора электрического смещения сквозь произвольную замкнутую поверхность равен алгебраической суме зарядов, охватываемых этой поверхностью.

Связь между векторами D и Е.

В случае изотропных диэлек­триков поляризованность 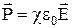. Подставив это соотношение в уравнение 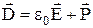, получим 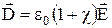, или 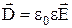, где e – диэлектрическая проницаемость вещества: 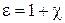. Диэлектрическая проницаемость является основ­ной электрической характеристикой диэлектрика. Для всех ве­ществ e > 1, для вакуума e = 1. Значения e зависят от природы диэлектрика.

Поле вектора D наглядно можно изобразить с помощью ли­ний вектора D, направление и густота которых определяются точно так же, как и для линий вектора Е. Линии вектора Е мо­гут начинаться и заканчиваться как на сторонних, так и на связанных зарядах. Источниками и стоками поля вектора D являются только сторонние заряды: только на них могут начинаться и заканчиваться линии вектора D. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.

Условия на границе двух диэлектриков.

Пусть на границе раздела двух диэлектриков находится поверхностный сторонний заряд. Терема о циркуляции вектора напряженности и теорема Гаусса для вектора 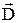имеют вид:

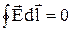и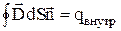

Условие для вектора 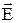. Пусть поле вблизи границы раздела в диэлектрике 1 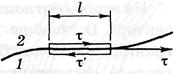равно 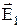, а в диэлектрике 2 – 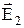. Возьмем небольшой вытянутый прямоугольный контур пренебрежимо малой толщины. Согласно теореме о циркуляции вектора напряженности 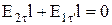, где проекции вектора напряженности взяты на направление обхода контура, указанное на рисунке стрелками. Если на нижнем участке контура проекцию вектора 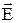взять не на орт 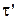а на общий орт t, то 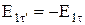и 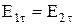, т. е. тангенциальная составляющая вектора напряженности оказывает­ся одинаковой по обе стороны границы раздела.

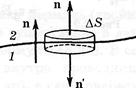
Условие для вектора 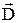. Возьмем очень малой высоты цилиндр, расположив его на границе раздела двух ди­электриков. Сечение цилиндра должно быть таким, чтобы в пределах каждого его торца вектор 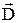был одинаков. Тогда согласно теореме Гаусса для вектора D 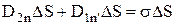, где s – поверхностная плотность стороннего заряда на границе раздела. Взяв обе проекции вектора 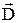на общую нормаль 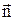, получим: 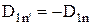, и предыдущее уравнение приобретает вид:

.

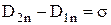Из полученного уравнения следует, что нормальная составляющая вектора 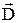претерпевает скачок при переходе границы раздела. Однако если сторонние заряды на границе раздела отсутствуют, то в этом случае нормальные составляющие вектора 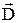скач­ка не испытывают, они оказываются одинаковыми по разные стороны границы раздела.

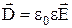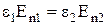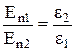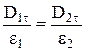Учитывая, что , получаем: или и или .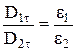

Таким образом, если на границе раздела двух одно­родных изотропных диэлектриков сторонних зарядов нет, то при переходе этой границы составляющие 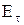и 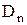изменяются непрерывно, без скачка, а составляющие 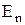и 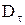претерпевают скачок.

Дата добавления: 2014-11-24; просмотров: 820; Нарушение авторских прав

Мы поможем в написании ваших работ!