Работа, мощность и энергия

Энергия E – единая мера оценки и сравнения различных форм движения. Она характеризует способность тела совершать работу.

Принципиально возможны два качественно различных способа передачи движения, т.е. Е, в форме работы А и в форме теплоты Q. Следовательно: [E]=[A]=[Q]=Н×м =Дж;

Передача энергии Е в виде А характеризуется перемещением макротел.

Передача энергии в виде Q происходит из-за разности температур макротел и идет только на изменение их внутренней структуры (E=A+Q). Следовательно, она характеризует способность тела совершать работу.

Полная Е взаимодействия тел состоит из двух частей: кинетической Е_к и потенциальной Е_{п .}

Кинетическая Е_к зависит только от скорости движения тел и не зависит от их положения в пространстве.

Потенциальная Е_п зависит только от начального и конечного положений тел, не зависит от скорости их движения.

Мощность N – количество работы, совершаемой за единицу времени (за 1 с), т.е. N = A/t; следовательно: [N] = Дж/с = Вт.

Работа, как физическая величина (в отличие от физиологического понятия, связанного с мускульной Е человека), характеризует действие силы через величину вызванного ею перемещения =>A= 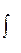FdsCos 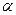; A = FSсos 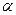, где могут быть случаи: F=сonst, F=var (нарисовать графики).

Работа консервативных сил (сил, не зависящих от траектории, по которой движется тело)- сил, действующих на расстоянии (гравитационных, электрических полей) зависит только от начального и конечного положений тела, Например, Р = mg.

Работа консервативных сил на замкнутом пути (контуре) равна нулю.

Связь между Е и А следует из F= m×a. Умножив обе части равенства на ds и помня, что ds=vdt, получим Fds = mavd t= mvdv.

Тогда, согласно определениям, имеем dA=Fds; dE_к = mvdv, откуда после интегрирования получаем A=F S сos 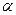; E_к=mv²/2- кинетическая энергия.

Если сos 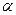>0, A>0 - работа положительная.

Если сos 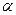<0, A<0 - работа отрицательная.

E_п=A=FS, при сos 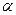=1 и вертикальном направлении движения (обычно принимают S = h), т.е. E_п = mgh – потенциальная энергия.

Полная энергия тела выразится уравнением E=E_к+E_п.

Следовательно, E=mv²/2+mgh;

Кинетическая энергия тела, вращающегося вокруг своей оси:

E_вр= S(m_iv_i)²/2 = Sm_i(wr_i)²/2 = (w²)/2Sm_ir_i² = J_zw²/2.

Кинетическая энергия тела, скатывающегося по наклонной плоскости, включает две составляющие: поступательного (mv²/2) и вращательного (J_cw²)/2 движений.

Следовательно, E_вр=(mv_c²)/2 + (J_cw²)/2.

Закон сохранения энергии вытекает из F=ma, m(dv/dt) =F_вну+F_вне; ds = vdt; mvdv = (F_вну+F_вне)ds; откуда mvdv - F_внуds = F_внеds, следовательно: 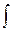mvdv = mv²/2 = E_к;

F_вну ds = F_вну S = F_вну h = E_п.

Так как F_вну зависит от взаимного расположения тел внутри системы, то имеем

dE_к+ dE_п = dA и, при отсутствии внешних сил F_вне =0, получим:

d(E_к + E_п)=0; E_к + E_п = сonst - закон сохранения энергии.

Закон сохранения энергии ( E_к+E_п = E = сonst) справедлив:

а) для консервативных сил (внутренних и внешних), работа которых не зависит от траектории движения тел, а зависит только от их начального и конечного положения;

б) для диссипативных сил, работа которых зависит от пути (то есть по дороге может изменяться, например, сила трения).

Применение законов сохранения энергии и импульса в механических системах имеет важное практическое значение при исследовании взаимодействия тел, особенно при их соударении:

удар тел (соударение тел) – взаимодействие, которое длится очень короткое время;

классификация удара по величине коэффициента восстановления

K=V_n1/V_n,

где V_n1– нормальная составляющая скорости после удара, V_n– до удара: если K=1 – абсолютно упругие;

если K=0 – абсолютно неупругие; в случае 0<K<1– не вполне упругие удары;

общие уравнения для исследования всех видов удара:

m₁v₁+ m₂v₂= m₁¢u₁+ m₂¢u₂ – закон сохранения импульса;

m₁v₁²/2+m₂v₂²/2=m₁¢ (u₁)²/2 + m₂¢ (u₂)²/2 – закон сохранения кинетической энергии.

В приведенных уравнениях знак ( ¢ ) относится к состоянию тел после удара, но не означает нахождение первой производной.

а) удар абсолютно упругих тел (абсолютно упругий удар):

Поскольку деформация тел при абсолютно упругом ударе отсутствует (m₁= m₁¢; m₂ = m₂¢), то законы сохранения можно представить в виде:

m₁ (v₁²- u₁²) = m₂ (u₂²- u₂²) (1)

m₁ (v₁- u₁) = m₂ (u₂- v₂). (2)

Пользуясь уравнениями (1) и (2), найдем скорости движения тел u₁ и u₂ после удара:

1) Разделив первое уравнение на второе, получим

(v₁+ u₁) = (u₂+ v₂). (3)

Умножив (3) на m₂ , найдем:

m₂ (v₁+ u₁) = m₂ (u₂+ v₂). (4)

Решая совместно уравнения (2) и (4), найдем, что

u₁ = 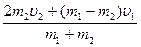. (5)

2) Умножив (3) на m₁ , найдем:

m₁ (v₁+ u₁) = m₁ (u₂+ v₂). (6)

Решая совместно уравнения (2) и (5), получим

u₂ = 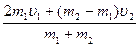. (7)

Частные случаи центральных упругих ударов (по уравнениям 5 и 7)

Тела имеют одинаковые массы (m₁= m₂), тогда из (5) имеем:

u₁ = 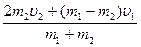= 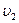; u₂ = =

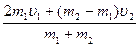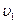
Из полученных уравнений следует, что тела “обменялись” скоростями.

Одно тело, например, второе – неподвижно, т.е. 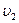=0, тогда

u₁ = 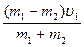; u₂ =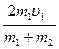

Из этих уравнений можно получить и другие частные случаи, когда:

m₁= m₂, m₂ 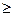m₁, m₁ 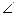m₂ и наоборот (посмотреть самостоятельно по Трофимовой, гл.3).

б) удар абсолютно неупругих тел (абсолютно неупругий удар):

В этом случае после столкновения тела объединяются и движутся как единое целое (u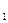=u =u 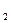). Тогда, на основании закона сохранения импульса, можно записать m₁v₁+ m₂v₂= (m₁+ m₂)u, откуда имеем

u =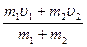

Частные случаи центральных неупругих ударов:

движение шаров равных масс навстречу друг другу:

так как m₁= m₂ = m, то

u = ;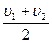

движение шаров разных масс навстречу друг другу:

u =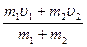

Вектор общей скорости u будет направлен в сторону движения тела, обладающего большим начальным импульсом.

Применение закона сохранения момента импульса: Известно: 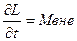; L= const, что возможно при М_вне= 0. Это является законом сохранения момента импульса (В замкнутой системе момент импульса не изменяется с течением времени).

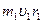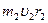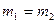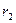
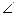
Скамья Жуковского – пример демонстрации закона сохранения момента импульса ( = ). При и уменьшении радиуса вектора приложения импульса ( 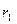) угловая скорость возрастает и наоборот. При этом направление вращения остается неизменным. Причиной таких изменений является изменение момента инерции вращающегося тела ( 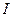= 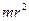), возникающего из-за рассредоточения или сосредоточения массы ввиду распрямления или сжатия рук.

Другие примеры:

гимнаст при прыжке через голову поджимает к туловищу руки и ноги, чтобы уменьшить свой момент инерции;

танцоры на льду используют принцип действия скамьи Жуковского.

Следовательно, L может измениться только при изменении М_вне: дать понятия о гироскопе, свободных осях вращения.

Заключительная часть

Боевой устав службы обязывает:

при спасении людей и прокладке рукавных линий выбирать кратчайшие пути;

обеспечить наиболее эффективное использование пожарной техники, своевременно снабжать пожарные машины горючим и смазочным материалами.

Рассмотренные в лекции зависимости позволяют грамотно выполнить требования руководящих документов.

Разработал профессор А.С.Поляков

Дата добавления: 2014-11-24; просмотров: 331; Нарушение авторских прав

Мы поможем в написании ваших работ!