Консервативные силы. Потенциальная энергия

В современном естествознании принято считать, что взаимодействие тел осуществляется посредством полей. Полем сил называют область пространства, в каждой точке которого на частицу действует сила, закономерно изменяющаяся от точки к точке. Другими словами, если в каждой точке пространства на материальную точку действуют силы, то говорят, что в пространстве действует силовое поле. Пример силового поля – поле силы тяжести. Пусть тело перемещается из точки 1 в точку 2 (рис. 5.3).

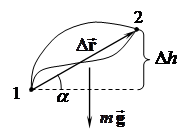
Рисунок 5.3 – Движение точки в поле силы тяжести

Вычислим работу, совершенную силой тяжести при этом перемещении. Согласно определению механической работы (5.1) мы можем записать:

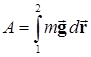. (5.10)

Теперь воспользуемся тем обстоятельством, что вблизи поверхности Земли сила тяжести постоянна: 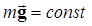. Постоянную величину можно вынести из-под знака интеграла, и выражение (5.10) для работы запишется так:

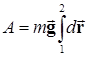. (5.11)

Интеграл в выражении (5.11) представляет собой сумму элементарных перемещений 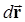, которые совершает тело при своем движении из точки 1 в точку 2. Очевидно, что сумма всех элементарных перемещений будет равна 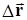. Следовательно, выражение (5.11) принимает вид

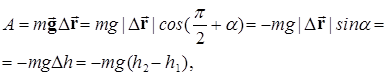(5.12)

где h₁ – высота, на которой находится тело над поверхностью Земли в начальном положении 1, а h₂ – высота в конечном положении 2. А теперь самое главное. При вычислении работы силы тяжести мы ничего не говорили о траектории, по которой движется наше тело. Очевидно, что для любой траектории, ведущей из точки 1 в точку 2, вектор перемещения 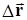будет один и тот же, и, согласно выражению (5.12), для всех траекторий работа силы тяжести будет иметь одно и то же значение. То есть работа силы тяжести не зависит от формы траектории, а определятся только начальной и конечной высотой тела над поверхностью Земли.

Силы, работа которых не зависит от формы траектории, по которой частица переходит из одного положения в другое, а определяется только начальным и конечным положением частицы, называются консервативными.[2] В этом случае каждому положению частицы в силовом поле можно сопоставить некоторую функцию 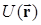, такую, что разность значений этой функции в точках 1 и 2 определяет работу сил поля по перемещению частицы между этими точками:

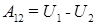. (5.13)

Функцию U называют потенциальной энергией частицы. Сравнивая формулы (5.12) и (5.13), мы приходим к выводу, что потенциальная энергия тела в поле силы тяжести описывается формулой

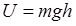, (5.14)

где h – высота, на которой находится тело над поверхностью Земли.

К консервативным силам относятся и силы упругости. Найдем потенциальную энергию упругой деформации. Сила упругости (см. лекцию 2, формула (2.10)) равна

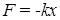. (5.15)

Здесь х – смещение конца пружины из положения равновесия. Если мы будем растягивать или сжимать пружину, то, на основании 3-го закона Ньютона, работа внешней силы, противоположно направленной силе упругости пружины, будет равна

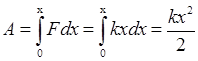. (5.16)

Эта работа внешней силы была затрачена на увеличение потенциальной энергии пружины. Если считать, что энергия пружины в недеформированном состоянии равна 0, то тогда:

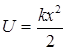. (5.17)

Потенциальную энергию часто называют энергией взаимодействия. Действительно, в первом примере взаимодействуют тело и Земля, в случае пружины взаимодействуют отдельные части одного тела (напомним, что силы упругости появляются при изменении взаимного расположения заряженных частиц, из которых состоит тело).

Еще один пример консервативных сил – центральные силы. Так называют силы, величина которых зависит только от расстояния между двумя частицами, а направлены они вдоль линии, соединяющей частицы. Центральными являются сила всемирного тяготения и сила Кулона (см. лекцию 2, формулы (2.5) и (2.6)). Для центральных сил элементарная работа 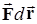будет равна

.

Соответственно, работа, совершаемая на конечном пути s, равна

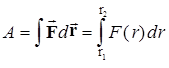. (5.18)

Из выражения (5.18) ясно, что полная работа зависит от начального и конечного расстояний от частицы до силового центра и не зависит от формы траектории. Подставим в формулу (5.18) выражение для силы всемирного тяготения (2.5):

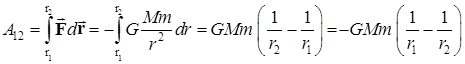. (5.19)

Знак “–” перед интегралом отражает тот факт, что направления силы и перемещения противоположны, если начало координат помещено на силовом центре. Из выражений (5.22) и (5.16) можно сделать вывод, что потенциальная энергия сил тяготения равна

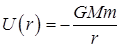. (5.20)

И ещё несколько слов о потенциальной энергии. Согласно выражению (5.13), работа консервативной силы будет равна убыли потенциальной энергии:

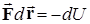. (5.21)

Расписывая скалярное произведение, получим:

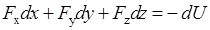. (5.22)

Если перемещение частицы происходило только вдоль x, в то время как y-я и z-я координаты оставались постоянными, то 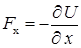. Здесь значок 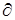означает частную производную по координате, которая берётся, когда остальные координаты остаются неизменными. Аналогичным образом получим компоненты сил F_y и F_z. Таким образом:

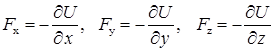. (5.23)

В соответствии с выражением (5.23) мы имеем 3 проекции силы на оси координат. Если умножим их на соответствующие единичные вектора и сложим, то получим вектор силы:

, (5.24)

или в сокращённом виде

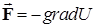. (5.25)

Здесь подразумевается, что

.

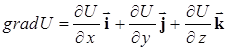В соответствии с выражением (5.25) gradU является вектором (читается “градиент U”), хотя функция U является скаляром. Наряду с выражением (5.25) используется обозначение ÑU: 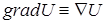, где Ñ (набла) – дифференциальный оператор, также называемый оператором Гамильтона, есть:

.

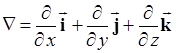Отметим, что grad какой-либо скалярной функции, как это доказывается в высшей математике, определяет направление наиболее быстрого роста этой функции. Если это свойство градиента скалярной функции применить к потенциальной энергии, то из уравнения (5.25) следует, что консервативные силы всегда направлены в сторону наиболее быстрого уменьшения потенциальной энергии.[3]

Дата добавления: 2014-07-11; просмотров: 694; Нарушение авторских прав

Мы поможем в написании ваших работ!