Закон сохранения механической энергии. Пусть на частицу действуют только консервативные силы

Пусть на частицу действуют только консервативные силы. Тогда, с одной стороны, работа по перемещению частицы из точки 1 в точку 2 определяется выражением (5.13) A₁₂ = U₁-U₂, а с другой стороны, эта работа определяет изменение кинетической энергии (5.6) A₁₂=T₁-T₂. Следовательно,

T₂ – T₁=U₁ – U₂ , или T₁ + U₁ = T₂ + U₂. (5.26)

Таким образом, мы получили, что величина E=T + U, для частицы, которая находится в поле действия консервативных сил, остаётся постоянной:

E = T + U = const.(5.27)

Физическая величина Е, равная сумме кинетической и потенциальной энергий частицы, называется полной механической энергией частицы. В соответствии с выражением (5.13) можно сказать, что работа совершается за счёт убыли потенциальной энергии частицы в поле консервативных сил, при этом эта работа, согласно выражению (5.6), идет на увеличение кинетической энергии частицы:

dT = – dU.

Пусть, кроме потенциальных сил, результирующая которых равна F, на частицу действует также и неконсервативная сила F*. Тогда при переходе частицы из положения 1 в положение 2 над ней будет совершаться работа:

.

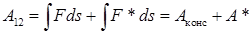В соответствии с теоремой о приращении кинетической энергии A₁₂ = dT, и, таким образом:

,

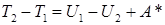или

E₂ – E₁ = A*.(5.28)

Таким образом, мы получили, что работа неконсервативных сил затрачивается на приращение полной механической энергии частицы.

Рассмотрим теперь систему частиц (тел), между которыми действуют консервативные силы и эта система находится во внешнем силовом поле консервативных сил [4], и, кроме того, пусть на частицы системы действуют неконсервативные силы. Тогда, как мы уже знаем, приращение кинетической энергии каждой частицы равно алгебраической сумме работ, которые совершают все силы:

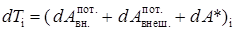, (5.29)

где индекс i обозначает номер частицы. С учётом того, что работу потенциальных сил можно представить как изменение потенциальной энергии частицы в соответствующем силовом поле:

,

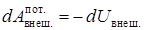
Выражение (5.29) можно переписать в виде

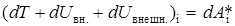. (5.30)

Введём понятие полной механической энергии системы как суммы кинетической и потенциальной энергий всех частиц системы:

.

Теперь, суммируя выражение (5.30) по всем частицам рассматриваемой системы, мы получим:

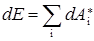. (5.31)

То есть, как и для одной частицы, полная механическая энергия системы частиц изменяется за счет работы только неконсервативных сил, которые действуют на отдельные частицы системы. Если неконсервативные силы отсутствуют, то из выражения (5.31) получаем:

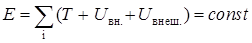. (5.32)

Следовательно, полная механическая энергия системы тел, на которые действуют только консервативные силы, остаётся постоянной. Это и есть закон сохранения полной механической энергии.

В теоретической физике доказывается, что закон сохранения полной механической энергии является следствием однородности времени. Однородность времени означает независимость физических законов от начала отсчёта времени, т.е. говорит нам о равнозначности всех моментов времени.

Особый случай неконсервативных сил представляют силы трения. Работа сил трения всегда отрицательна, так как силы трения направлены против вектора скорости:

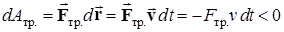. (5.33)

Согласно уравнению (5.33) полная механическая энергия системы при наличии трения уменьшается. Такой процесс называется диссипацией, или рассеянием энергии, а силы, которые приводят к потере механической энергии, называются диссипативными.

Кроме рассмотренной нами полной механической энергии в природе существуют другие виды энергии. Как вы знаете из повседневного опыта, при трении тела нагреваются, а это значит, что полная механическая энергия переходит во внутреннюю энергию («тепловую» энергию) взаимодействующих тел. В этом смысле уравнение:

DE = A*,

также является законом сохранения энергии, если известно, в какие формы переходит механическая энергия системы. Для энергии, как единой характеристики различных форм движения материи, справедлив закон сохранения энергии, который может быть сформулирован следующим образом: энергия никогда не уменьшается и не увеличивается, не исчезает и не появляется вновь, она лишь превращается из одного вида в другой.

[1] Подчеркнем еще раз, что в этой теореме речь идет о работе именно равнодействующей всех сил, действующих на тело, так как при выводе формулы (5.5) мы воспользовались вторым законом Ньютона.

[2] Другое название этих сил – потенциальные. Мы будем использовать эти термины как синонимы.

[3] Иллюстрацией этого утверждения является положение русел рек. Они всегда находятся в местах с наименьшей для данной местности потенциальной энергией поля силы тяжести.

[4] Например, электрически заряженные тела, которые находятся во внешнем электрическом поле.

Дата добавления: 2014-07-11; просмотров: 450; Нарушение авторских прав

Мы поможем в написании ваших работ!