Элементарная теория гироскопа

Пример

Тонкий однородный стержень массы 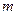и длины 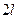прикреплен в центре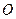к вертикальной оси. Вычислить моменты инерции стержня 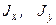и центробежный момент инерции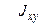. Оси координат показаны на рисунке.

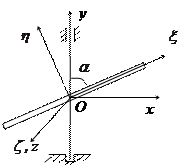Тензор инерции в базисе, связанном с главными осями, для тонкого однородного стержня

.

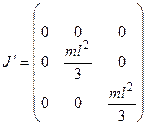Матрица перехода от системы координат 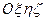к системе координат .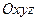

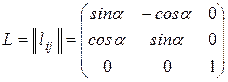Тогда для тензора инерции в новом базисе получаем 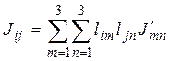или

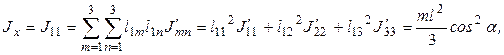
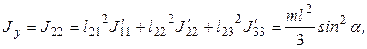
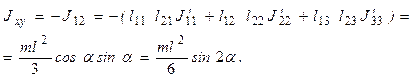
Аналогично определяются остальные элементы матрицы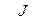

.

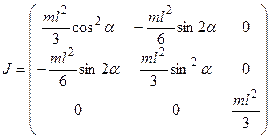Динамика вращательного и сферического движения

твердого тела

Левую часть в теореме об изменении кинетического момента можно рассматривать как абсолютную скорость точки − конца вектора 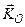. Движение этой точки можно рассматривать как сложное. Оно происходит за счет изменения вектора 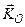в подвижной системе координат, жестко связанной с твердым телом, (относительное движение) и его поворота с угловой скоростью 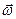по отношению к неподвижной системе координат (переносное движение). Тогда

,

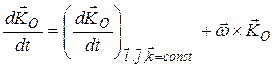где 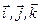- орты подвижной системы координат.

Подставляя это выражение в теорему об изменении кинетического момента 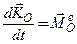и проектируя на оси подвижной системы координат, находим

,

,

.

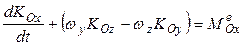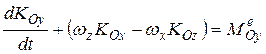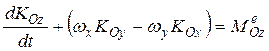При вращательном движении твердого тела (например, вокруг оси 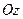) направление вектора угловой скорости остается постоянным 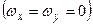. В этом случае имеем

,

,

.

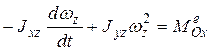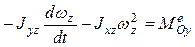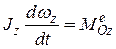Последнее равенство позволяет получить дифференциальное уравнение вращательного движения

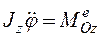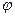, − угол поворота тела.

Первые два могут быть использованы для определения динамических реакций подшипников, когда ось вращения не является главной осью инерции (динамическая неуравновешенность).

В случае сферического движения, если в качестве подвижных осей взять главные оси инерции тела и ввести обозначения

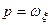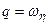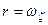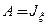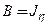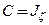,,; ,,, то

,

,

.

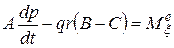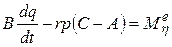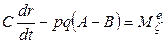Эти уравнения называются динамическими уравнениями Эйлера. Они допускают аналитическое интегрирование при произвольных начальных условиях движения в трех случаях.

1. Случай Эйлера – Пуансо. Центр масс тела произвольной формы совпадает с неподвижной точкой. Движение тела происходит по инерции.

2. Случай Лагранжа[1] – Пуассона[2]. Эллипсоидом инерции для неподвижной точки является эллипсоид вращения 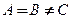и центр масс лежит на оси вращения эллипсоида инерции. (Симметричный волчок).

3. Случай Ковалевской[3]. Эллипсоид инерции для неподвижной точки есть вытянутый эллипсоид вращения при 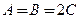. Центр масс тела лежит в экваториальной плоскости эллипсоида инерции. (Асимметричный волчок).

Уместно отметить, что кинетический момент относительно неподвижной точки и кинетическая энергия твердого тела при сферическом движении определяются выражениями:

,

.

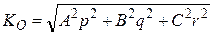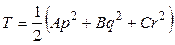В случае Эйлера-Пуансо два интеграла движения находятся непосредственно из законов сохранения кинетического момента и энергии

,

.

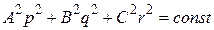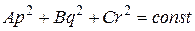Дифференциальные уравнения свободного движения твердого тела нетрудно получить, если к динамическим уравнениям Эйлера, для описания относительного движения тела вокруг центра масс, добавить уравнения движения центра масс.

Гироскоп - быстро вращающееся симметричное твердое тело, ось вращения которого (ось симметрии) может изменять свое направление в пространстве. Гироскопы обладают рядом интересных свойств, обусловливающих их широкое применение в различных технических устройствах. В качестве примера на рисунке изображены гироскоп с тремя степенями свободы, когда ротор может совершать три независимых вращения вокруг осей , пересекающихся в одной точке O (карданов подвес),

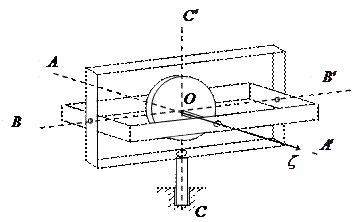
и гироскоп с двумя степенями свободы, когда ротор может вращаться только вокруг осей .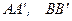

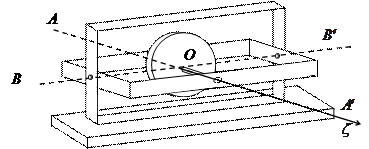Гироскопы совершают сферическое движение. Если неподвижная точка О совпадает с центром масс, то такой гироскоп называется астатическим (уравновешенным), в противном случае – тяжелым.

Элементарная или прецессионная теория гироскопа основана на допущении, что угловая скорость вращения гироскопа вокруг оси материальной симметрии значительно превышает угловую скорость поворота этой оси.

Пусть 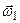- угловая скорость быстро вращающегося гироскопа, 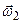- угловая скорость вращения оси гироскопа. В рамках прецессионной теории можно считать, что кинетический момент гироскопа относительно неподвижной точки направлен вдоль оси симметрии гироскопа 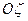и равен

.

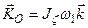Для установления основных свойств гироскопа докажем следующую теорему.

Теорема Резаля[4]

Теорема

Скорость конца вектора кинетического момента механической системы относительно некоторого неподвижного центра геометрически равна главному моменту внешних сил, действующих на эту систему, относительно того же центра.

Доказательство:

Пусть точка A - конец вектора 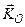. Скорость ее движения: 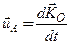. Сравнивая данное соотношение с теоремой об изменении кинетического момента, получим

.

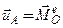Теорема доказана.

Отметим, что это кинематическая интерпретация теоремы об изменении кинетического момента.

Используя теорему Резаля, можно:

1. Зная внешние силы, найти, как движется ось гироскопа.

2. Зная движение оси гироскопа, можно найти главный момент внешних сил.

Основные свойства гироскопа

Рассмотрим установившееся вращательное движение с угловой скоростью 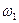астатического гироскопа с тремя степенями свободы. При этом главный момент внешних сил, действующих на гироскоп, относительно неподвижной точки равен нулю. Тогда по теореме об изменении кинетического момента

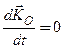или .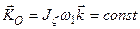

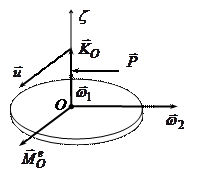
Т.е. вектор 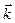, который задает положение оси гироскопа, остается постоянным по направлению в инерциальной системе отсчета, и имеет место следующее свойство:

Первое свойство астатического гироскопа

Ось быстро вращающегося уравновешенного (с тремя степенями свободы) гироскопа устойчиво сохраняет свое направление в инерциальной системе отсчета. Удары или толчки могут вызвать вибрацию оси гироскопа, но не отклонение от первоначального положения.

Это свойство широко используется в различных навигационных приборах и стабилизаторах движения. Второе свойство гироскопа обнаруживается, когда на его ось начинает действовать сила (или пара сил), стремящаяся привести ось в движение

Пусть на ось гироскопа действует постоянная сила 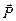, как указано на рисунке.

По теореме Резаля: .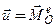

Т.е. действие постоянной силы на ось гироскопа приводит к повороту этой оси с некоторой угловой скоростью 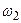. По формуле Эйлера для скорости точки, совпадающей с концом вектора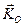

.

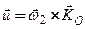С учетом равенства 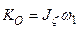из теоремы Резаля находим

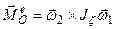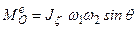или , где 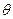− угол нутации.

Движение, совершаемое осью гироскопа от постоянной силы, называется прецессией. 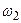- угловая скорость прецессии

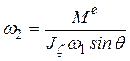− закон прецессии.

Это равенство выражает следующее свойство.

Второе свойство гироскопа

При действии силы (или пары сил ) на ось быстро вращающегося гироскопа она будет отклоняться не в сторону действия силы, как это было бы при невращающемся роторе, а в направлении, перпендикулярном этой силе. При этом вращение оси будет происходить с постоянной угловой скоростью.

Данное свойство наблюдается как у астатического, так и тяжелого гироскопа.

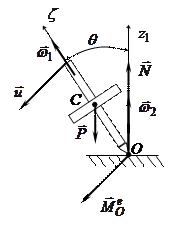Пример. Рассмотрим движение волчка. Действующие на него внешние силы - сила тяжести 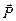и сила реакции .

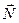Главный момент внешних сил: .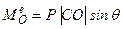

Из закона прецессии

.

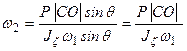Угловая скорость прецессии тем меньше, чем больше угловая скорость вращения волчка вокруг его оси симметрии.

Регулярная прецессия - движение гироскопа с постоянными угловыми скоростями собственного вращения, прецессии и постоянным углом нутации.

Момент гироскопических реакций.

Рассмотрим движение астатического гироскопа с двумя степенями свободы, когда ось гироскопа принудительно поворачивается.

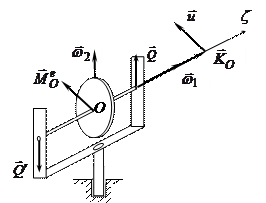В этом случае главный момент внешних сил, действующих на гироскоп, отличен от нуля

.

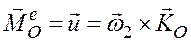Силы, создающие этот момент − силы гироскопических реакций в подшипниках. Противоположный момент создают силы давления на подшипники .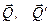

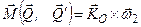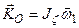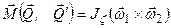. Так как , то или ,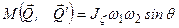

где 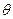− угол между осью собственного вращения гироскопа и осью прецессии.

Под действием гироскопической пары сил давления на подшипники система может перемещаться. Пара сил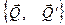стремится совместить ось вращения гироскопа с осью прецессии. Данный результат можно сформулировать в виде следующего правила.

Правило Жуковского

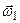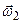Если гироскопу сообщают вынужденное прецессионное движение, то возникает гироскопическая пара сил давления на подшипники, стремящаяся кратчайшим путем установить ось гироскопа параллельно оси прецессии так, чтобы векторы и совпадали.

Возможность возникновения гироскопических реакций при вынужденной прецессии быстро вращающихся деталей машин (например, роторов судовых и авиационных двигателей) необходимо учитывать в инженерных расчетах.

Литература: [1, §57, 102-105, 131, 132]; [2, §34-41, 88-95]; [3, п. 12.1-12.9, 13.4, 14.1, 15.1-15.6].

[1] Лагранж Жозеф Луи (25.01.1736-10.06.1813) − французский математик и механик, член Французской АН, член и президент Берлинской АН. Труды по вариационному исчислению, математическому анализу, теории чисел, алгебре и дифференциальным уравнениям. Написал трактат «Аналитическая механика».

[2] Пуассон Симеон Дени (21.06.1781-25.04.1840) − французский математик и механик, член института Франции, почетный член Петербургской АН. Работы посвящены теории рядов Фурье, теории неопределенных интегралов, вариационному исчислению, теории вероятностей, математической физике, теоретической механике. Написал «Курс механики».

[3] Ковалевская Софья Васильевна (15.01.1850-10.02.1891) − русский математик и механик, чл.-кор. Петербургской АН. Доктор философии Геттингенского университета. Профессор Стокгольмского университета. Исследования относятся к динамике, математической физике, небесной механике, теории дифференциальных уравнений; наиболее важные − к теории вращения твердого тела. Автор литературных произведений.

^[4] Резаль Анри Эме (27.01.1828-22.08.1896) − французский ученый в области механики, член Парижской АН. Работы посвящены вопросам механики, баллистики и термодинамики.

Дата добавления: 2014-02-27; просмотров: 1163; Нарушение авторских прав

Мы поможем в написании ваших работ!