ТВЕРДОГО ТЕЛА

СФЕРИЧЕСКОГО ДВИЖЕНИЯ

ДИНАМИКА ВРАЩАТЕЛЬНОГО И

1. Геометрия масс.

2. Динамика вращательного и сферического движения твердого тела.

3. Элементарная теория гироскопа.

Геометрия масс

Прежде чем приступить к изучению динамики вращательного и сферического движения твердого тела, рассмотрим выражение кинетического момента твердого тела в общем случае его сферического движения

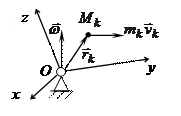
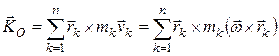, где 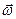− мгновенная угловая скорость сферического движения.

В проекциях на оси системы координат, связанной с движущимся телом,

,

,

.

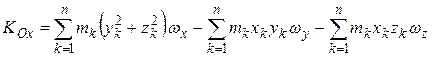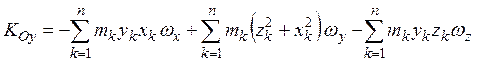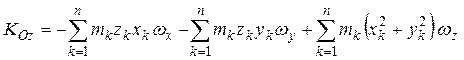Так как 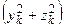, , 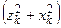− квадраты расстояний от точки с массой 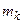до координатных осей 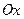, , 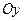, 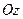то 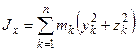, , 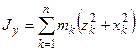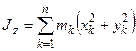− осевые моменты инерции.

Введем обозначения:

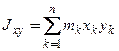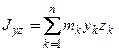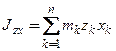, , − центробежные моменты инерции(, , ).

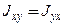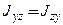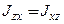Тогда ,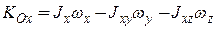

,

.

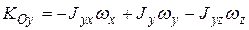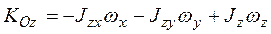В общем случае вектор кинетического момента не совпадает по направлению с вектором угловой скорости. В матричном виде эта связь записывается выражением

.

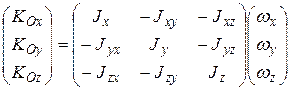Или как линейное преобразование трехмерного пространства: 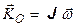, где 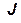− линейный оператор в этом пространстве.

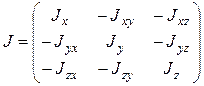
Матрица 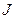является симметричной и ее элементы определяются моментами инерции твердого тела, характеризующими распределение масс относительно координатных осей.

Как известно, при изменении базиса (преобразовании системы координат) матрицу линейного преобразования можно привести к диагональному виду ,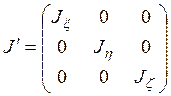

где 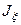,,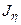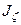− собственные значения линейного оператора 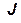, которые находятся из уравнения

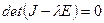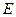, − единичная матрица.

Соответствующие ос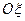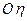и ,и 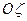называются главными осями инерции твердого тела. Если начало координат совпадает с центром масс, то они называются главными центральными осями инерции. Главной осью инерции, кроме того, по определению называется ось координат, для которой центробежные моменты инерции, содержащие индекс этой оси, равны нулю. Например, если 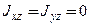, то 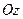− главная ось инерции. Если она проходит через центр масс, то ее называют главной центральной осью инерции. Из определения центробежных моментов инерции следует: ось симметрии однородного тела является главной для всех точек данной оси; для точек, лежащих в плоскости материальной симметрии, главной является ось, перпендикулярная этой плоскости. Для точек, лежащих на главных центральных осях инерции тела, главные оси инерции параллельны главным центральным осям инерции.

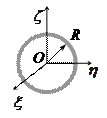
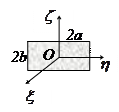
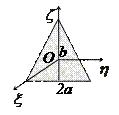
Моменты инерции однородных пластинок

в главных центральных осях

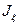
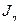
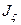
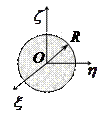
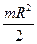
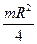
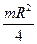
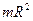
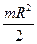
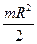
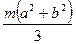
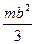
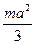
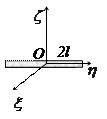
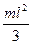
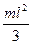
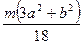
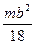
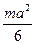
Одно и то же линейное преобразование в двух разных базисах имеет разные матрицы 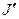и 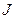. Используя традиционную нумерацию координатных осей, обозначая через 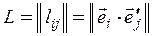ортогональную матрицу перехода от базиса (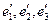), соответствующего главным осям, к базису (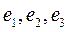) с произвольным расположением базисных векторов, имеем

,

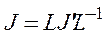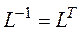
(в силу ортогональности обратная матрица совпадает с транспонированной).

Тогда связь между элементами матриц 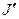и 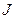можно записать в ви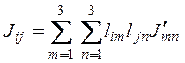де

, где 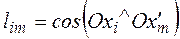− косинусы углов между новыми и старыми осями.

В частности, момент инерции относительно произвольной оси 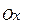, составляющей углы 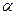,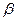и 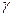с главными осям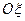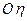и ,и 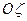, в соответствии с указанным правилом перехода от одного базиса к другому определится равенством

.

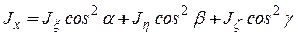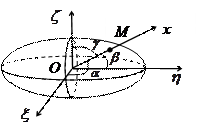
Этому равенству можно дать геометрическую интерпретацию. Вдоль оси 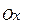отложим отрезок 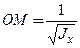. Координаты точки 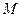равны

, , .

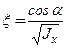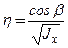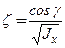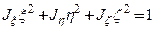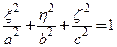Тогда или , где , , .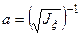

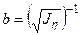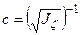Геометрическим местом точек 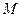является поверхность эллипсоида, называемого эллипсоидом инерции, с полуосями, обратными корням квадратным из соответствующих главных моментов инерции. Каждой точке твердого тела можно сопоставить эллипсоид инерции. По построению, длина отрезка, соединяющего данную точку с произвольной точкой поверхности эллипсоида, обратно пропорциональна корню квадратному из момента инерции твердого тела относительно оси соответствующего направления. Вместе с массой эллипсоид инерции полностью определяет инертные свойства твердого тела.

Напомним, что связь между моментами инерции относительно параллельных осей, одна из которых проходит через центр масс, дается теоремой Гюйгенса-Штейнера 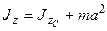, где 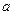− расстояние между осями.

Действительно:

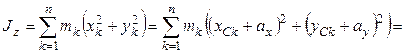
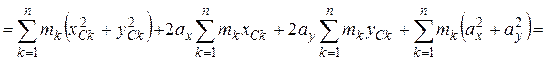
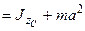, так как 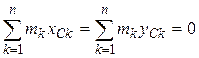по определению центра масс.

Дата добавления: 2014-02-27; просмотров: 346; Нарушение авторских прав

Мы поможем в написании ваших работ!