
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Момент импульса твердого тела
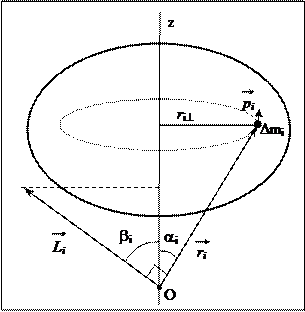
Рассмотрим твердое тело, которое вращается вокруг неподвижной оси z с угловой скоростью w. Выделим в теле малую частицу массой Dmi. Найдем момент импульса этой частицы относительно некоторой точки О на оси вращения z. Если радиус-вектор частицы 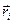 , вектор импульса
, вектор импульса 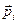 , то вектор момента импульса частицы
, то вектор момента импульса частицы 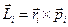 приложен к точке О и направлен перпендикулярно к векторам
приложен к точке О и направлен перпендикулярно к векторам 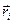 и
и 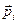 , т.е. под некоторым углом bi к оси z. Траекторией частицы Dmi является окружность, поэтому вектор импульса
, т.е. под некоторым углом bi к оси z. Траекторией частицы Dmi является окружность, поэтому вектор импульса 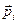 направлен по касательной к этой окружности. Следовательно, угол между векторами
направлен по касательной к этой окружности. Следовательно, угол между векторами 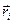 и
и 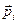 равен 900 (как угол между образующей и направляющей конуса). Тогда величина момента импульса частицы:
равен 900 (как угол между образующей и направляющей конуса). Тогда величина момента импульса частицы: 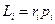 .
.
Пусть 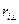 - радиус окружности – траектории частицы. Тогда
- радиус окружности – траектории частицы. Тогда 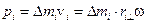 . Рассмотрим проекцию вектора момента импульса этой частицы на ось z:
. Рассмотрим проекцию вектора момента импульса этой частицы на ось z: 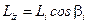 .
.
Учитывая, что 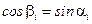 , получаем:
, получаем: 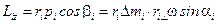 . Но
. Но 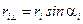 . Тогда
. Тогда
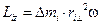 .
.
Для всего тела: 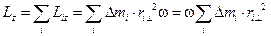 .
.
 В это выражение входят параметры движения частиц, которые не зависят от положения точки О. Поэтому момент импульса тела относительно оси z не зависит от положения точки О на оси. В соотношении для
В это выражение входят параметры движения частиц, которые не зависят от положения точки О. Поэтому момент импульса тела относительно оси z не зависит от положения точки О на оси. В соотношении для 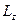 величина
величина 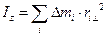
называется моментом инерции твердого тела относительно оси z (единица измерения кг×м2). Тогда можно записать: 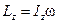 .
.
Зависимость для величины 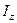 показывает, что момент инерции твёрдого тела зависит от распределения масс относительно оси вращения. Для сплошных тел суммирование можно заменить интегралом по массе тела:
показывает, что момент инерции твёрдого тела зависит от распределения масс относительно оси вращения. Для сплошных тел суммирование можно заменить интегралом по массе тела:
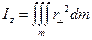 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Момент импульса механической системы | | | Твердого тела вокруг неподвижной оси |
Дата добавления: 2014-03-04; просмотров: 479; Нарушение авторских прав

Мы поможем в написании ваших работ!