
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Момент импульса механической системы
Рассмотрим суммарный момент импульса системы точек (тела) относительно некоторой точки О:
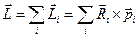 .
.
При переходе к другой точке О1 радиус-векторы точек системы преобразуются по правилу: 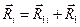 , поэтому
, поэтому
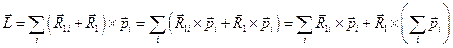 .
.
Суммарный импульс системы равен импульсу центра масс: 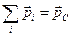 , тогда
, тогда 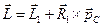 .
.
Поэтому в системе отсчета, где центр масс тела покоится: 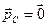 , суммарный момент импульса не зависит от точки, относительно которой он вычисляется.
, суммарный момент импульса не зависит от точки, относительно которой он вычисляется.
Если рассматривается движение твердого тела, то возможное движение в случае 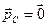 – это вращение вокруг центра масс. В этом смысле момент импульса описывает вращательное движение системы точек (тела).
– это вращение вокруг центра масс. В этом смысле момент импульса описывает вращательное движение системы точек (тела).
Найдем производную по времени от суммарного момента импульса механической системы:
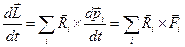 .
.
Силы, действующие на точки системы, разделим на внутренние, действующие между точками системы и внешние – со стороны тел, не входящих в систему: 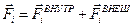 .
.
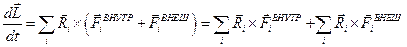 .
.
Внутренние силы подчинятся третьему закону Ньютона - они лежат на прямых линиях, попарно соединяющих точки, противоположны по направлению и одинаковы по величине:
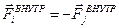 .
.
Для каждой из таких пар сил можно ввести одинаковое плечо 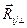 , поэтому
, поэтому
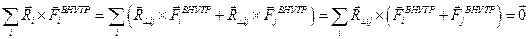 .
.
Окончательно получаем:
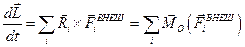 .
.
Уравнение динамики вращательного движения системы точек:
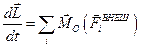 .
.
Производная от вектора суммарного момента импульса системы равна векторной сумме моментов внешних сил, действующих на систему.
Это уравнение часто называют уравнением моментов.
Покоординатное равенство:
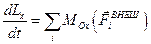 ,
, 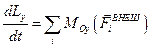 ,
, 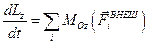 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Момент силы относительно оси | | | Момент импульса твердого тела |
Дата добавления: 2014-03-04; просмотров: 534; Нарушение авторских прав

Мы поможем в написании ваших работ!