
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОСНОВЫ ТЕОРИИ ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Итак, будем рассматривать теорию статистических гипотез на примере:
Допустим, мы проводим исследовательскую работу по работоспособности. На основе изученной литературы, мы предположили что показатели работоспособности в видах спорта с более высокой двигательной активностью будут выше чем в менее активных видах спорта.
Мы решили провести исследование на футболистах и волейболистах. Выдвигаем гипотезу: Ввиду того что футбол является более активным видом спорта чем волейбол мы предполагаем что футболисты обладают повышенной работоспособностью в сравнении с волейболистами.
Произведена выборка волейболистов и футболистов одной классификации примерно одного возраста.
В качестве контрольного теста на работоспособность нами был выбран тест PWC 170.
Приведём расчёты для сравнения групп (n1=n2=12) юных спортсменов-волейболистов и футболистов по показателям работоспособности согласно тесту PWC170/кг массы тела.
| № | волейбол | футбол | ||
| ФИО | PWC170/кг | ФИО | PWC170/кг | |
| 1. | А. Владислав | 21,5 | Б.Денис | 20,0 |
| 2. | В. Леонид | 17,3 | Б. Максим | 23,7 |
| 3. | Е. Алексей | 18,2 | В. Кирилл | 17,1 |
| 4. | К. Дмитрий | 19,0 | Г. Илья | 22,5 |
| 5. | К. Николай | 22,3 | Ж. Роман | 23,8 |
| 6. | К. Константин | 17,9 | К. Александр | 21,8 |
| 7. | Р. Андрей | 19,0 | М. Сергей | 24,3 |
| 8. | Р. Владимир | 17,1 | О. Алексей | 20,4 |
| 9. | Ш. Кирилл | 20,2 | П. Олег | 20,6 |
| 10. | К. Евгений | 21,1 | С. Илья | 21,6 |
| 11. | М. Егор | 24,8 | Ш. Дмитрий | 23,2 |
| 12. | П. Илья | 19,6 | Щ. Артём | 19,3 |
Согласно методике статистических гипотез мы выдвигаем статистическую гипотезу.
Статистической гипотезой - называется предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки. Статистическую гипотезу обозначают символом H
Проверка статистических гипотез состоит из 6 этапов:

Приступаем к работе согласно схеме.
1.Формулируем гипотезы:
Альтернатавная гипотеза (Н1): Мы предпологаем что средний паказатель работоспособности футболистов будет выше чем у волейболистов.
Основная гипотеза(Н0) соответственно будет свидетельствовать об обратном. т.е. работоспособность у футболистов будет ниже или ровна волейболистам.
Н0:`х ≥`y
Н1: `x <`y
где: `х- среднее арифметическое волейболистов
`y- среднее арифметическое футболистов.
2. Задаем уровень значимости:
Уровнем значимости - α гипотезы называют вероятность совершить ошибку первого рода, то есть отклонить верную нулевую гипотезу.
Значение α обычно выбирается небольшим: 10% - 0,1; 5% - 0,05 или 1% 0,01. В педагогике считается достаточным 5% .
α=0,05
3.Выбираем статистику – критерий проверки гипотезы.


 Критерий с помощью которого мы будем проверять нашу гипотезу выбирается исходя из свойств выборки.
Критерий с помощью которого мы будем проверять нашу гипотезу выбирается исходя из свойств выборки.
 |  | ||||
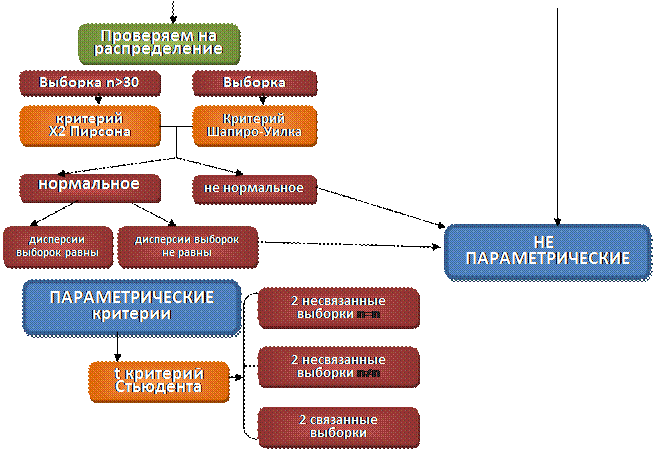 |
- наши данные измерены в шкале порядка
- выборка(n) = 12 человек
- применяем критерий Шапиро-Уилка для определения нормальности выборки (применение критерия рассмотрим ниже).
Наши данные нормально распределены.
- сравниваем дисперсии выборок с помощью критерия Фишера (см. ниже)
Дисперсии одинаковые.
Все условия для использования параметрического критерия соблюдены, используем t критерий Стьюдента. Данных одинаковое количество nx=ny соответственно используем формулу для 2 несвязных выборок n=n.
4.Определяем критическую область.
Критическая область определяется исходя из вида основной гипотезы (Н0)
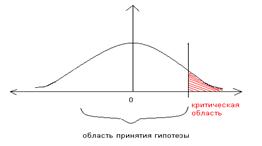 Н0:`х ≥`y
Н0:`х ≥`y
у нас будет правосторонняя критическая область
Определяем по таблице приложения критическое значение для соответствующего уровня значимости α и данного числа степеней свободы tкр=( α;n+n-2). Смотрим по таблице Стьюдента tкр = точка с координатами (0,05;10+10-2).
tкр =2,07
5.Определяем значение статистики по выборке.
Используем формулу tкритерия Стьюдента для несвязанных выборок с одинаковым количеством испытуемых (n=n)
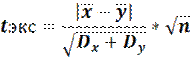
· Находим средние арифметические:
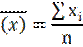
`х=19,8 `y=21,5
· Находим дисперсии:
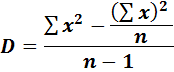 т.к n<30
т.к n<30
Dx=5.12 Dy=4.55
· высчитываем критерий:

6.Сравниваем с критической областью и делаем выводы.
tэкс(1.88)< tкр(2,07)
таким образом различия в средних значениях работоспособности не существенны на уровне значимости α=0,05.
ВЫВОД: Соответственно наша гипотеза не подтвердилась, волейболисты и футболисты, по крайней мере этого возраста и этой квалификации, достоверно не различаются по уровню работоспособности.
Пример для самостоятельной работы:
Время простой двигательной реакции футболистов 9 и 14 лет.(n=20и n=12)
Мы предполагаем что у футболистов 9 и 14лет время двигательной реакции будет различаться.
9-летние`х=373 14-летние`y=257,3
Обратите внимание что группы испытуемых не равны.
Н0: х+у Н1:х≠у
Dx=1316.8 Dy=642.8
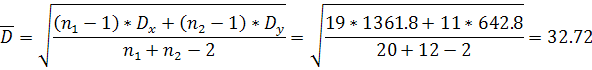
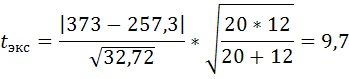
t кр=(0,05;20+12-2)=2,04
tэкс(9,7) >tкр(2,04)
Вывод: Двигательная реакции футболистов 9 и 14 лет будут значительно различаться при значимости 5%
| <== предыдущая страница | | | следующая страница ==> |
| ЗАНЯТИЕ 6. Семинар-диспут. Тема 6: Общая характеристика ювенального права | | | Семинарское занятие №4 Философия Ф.Бэкона |
Дата добавления: 2014-11-24; просмотров: 389; Нарушение авторских прав

Мы поможем в написании ваших работ!