
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ТЕОРИЯ ВЕРОЯТНОСТЕЙ математики
Справочный материал.
Случайные события:
- вероятность события P(A) = 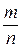 , n – число всех единственно возможных и равновозможных исходов испытания, а m – число исходов благоприятствующих появлению события А;
, n – число всех единственно возможных и равновозможных исходов испытания, а m – число исходов благоприятствующих появлению события А;
Pn= n! - число перестановок n различных элементов
( n! = 1 ∙ 2 ∙ 3 ∙ 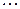 ∙ n, при этом 0! = 1 );
∙ n, при этом 0! = 1 );
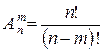 число размещений m различных элементов в n местах
число размещений m различных элементов в n местах
(m ≤ n);
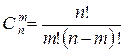 число сочетаний по m элементов из n различных
число сочетаний по m элементов из n различных
элементов ( m ≤ n, 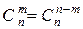 );
);
А + В – это событие, состоящее в появлении А или В или А и В вместе;
А ∙ В – это событие, состоящее в появлении А и В вместе;
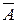 – это событие противоположное А;
– это событие противоположное А;
Р(А+В) = Р(А) + Р(В) для несовместных событий А и В;
Р(А+В) = Р(А) + Р(В) − Р(А∙В) для совместных событий А и В;
Р(А∙В) = Р(А) ∙ Р(В) для независимых событий А и В;
Р(А∙В) = Р(А)∙Р 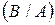 для зависимых событий А и В, где Р
для зависимых событий А и В, где Р 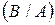 – условная вероятность появления события В при условии, что событие А
– условная вероятность появления события В при условии, что событие А
уже появилось;
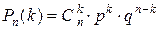 формула Бернулли для вычисления вероятности появления события А ровно
формула Бернулли для вычисления вероятности появления события А ровно 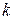 раз в серии из n испытаний, при этом
раз в серии из n испытаний, при этом
Р(A) = p в каждом испытании, Р( 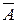 ) = q, p + q = 1;
) = q, p + q = 1;
Р(А) = 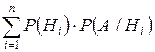 - формула полной вероятности, при этом гипотезы Hiобразуют полную группу событий, то есть они попарно
- формула полной вероятности, при этом гипотезы Hiобразуют полную группу событий, то есть они попарно
независимы и 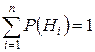 , а событие А происходит только с одной из гипотез Hi;
, а событие А происходит только с одной из гипотез Hi;
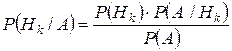 - формула Байеса для вычисления вероятности гипотезы Нк при условии, что событие А произошло.
- формула Байеса для вычисления вероятности гипотезы Нк при условии, что событие А произошло.
Случайные величины.
Дискретная случайная величина (ДСВ):
X принимает изолированные числовые значения x1, x2 , .... ;
- ряд распределения ДСВ – это таблица вида:
| xi | x1 | x2 | .... |
| Pi | P1 | P2 | ... |
при этом 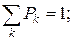
- многоугольник распределения – это ломаная, соединяющая точки ( 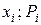 );
);
- интегральная функция F(x) = P(X < x) = F(a) + P(a ≤ X < x) представляет собой ступенчатую кривую;
- математическое ожидание ДСВ определяется формулой 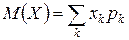 ;
;
- свойства: M(С) = C, M(hX + C) = h ∙M(X) + C;
- дисперсия D(X) = M(X − M(X))² = M(X²) − M²(X);
- расчетные формулы: D(X) 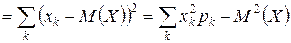 ;
;
- свойства: D(X) ≥ 0, D(0) = 0, D(h∙X + c) = h² ∙D(X);
- среднее квадратическое отклонение 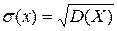 ;
;
Основные виды распределений ДСВ.
1. Геометрическое: X = k = 1, 2, 3...
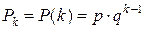 ,
,
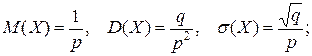
2. Распределение Бернулли (биноминальное): X = k = 0, 1, 2, ..... , n
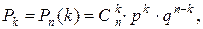
M(X) = n ∙ p, D(X) = n ∙ p ∙ q, 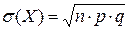 ;
;
3. Распределение Пуассона: X = k = 0, 1, 2, ... , n
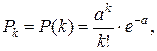
M(X) = a, D(X) = a, 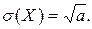
Непрерывная случайная величина (НСВ):
X принимает числовые значения 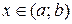 ;
;
- плотность (дифференциальная функция) распределения вероятностей: 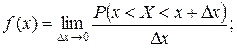
- интегральная функция распределения:
F(x) = P(X < x) = 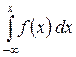 , при этом
, при этом  ;
;
- вероятность попадания НСВ в интервал
P(α < X < β) = F(β) – F(α) = 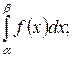
- математическое ожидание M(X) = 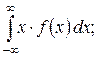
- дисперсия D(X) 
- среднее квадратическое отклонение 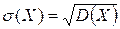 .
.
Основные виды распределений НСВ:
1. Равномерное распределение в интервале (a, b)
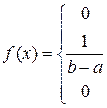 при
при 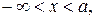
при 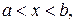
при 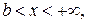
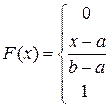
при 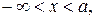
при a 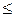 x
x 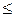 b,
b,
при  ,
,
M(X) =  D(X) =
D(X) = 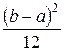 ,
, 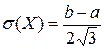 ;
;
1. Показательное распределение
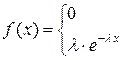 при
при 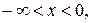
при 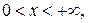
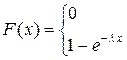 при
при 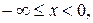
при 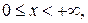
M(X) = 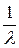 , D(X) =
, D(X) = 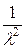 ,
, 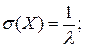
2. Нормальное распределение
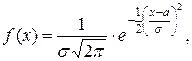
F(x) = 0.5 + Ф( 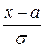 ), где Ф(z) =
), где Ф(z) = 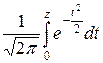 – функция Лапласа (ее значения имеются в приложениях учебников по теории вероятностей);
– функция Лапласа (ее значения имеются в приложениях учебников по теории вероятностей);
M(X) = a, D(X) = 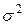 ,
, 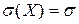 ,
,
P(α < X < β) = Ф 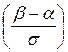 – Ф
– Ф 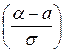 .
.
Примеры.
1. Из разрезной азбуки сложено слово МАМА, затем рассыпано и сложено случайным образом. Найти вероятность того, что снова получится слово МАМА.
P = 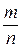 , n = P4= 4! = 24, m = 2! ∙ 2! = 4 => P =
, n = P4= 4! = 24, m = 2! ∙ 2! = 4 => P = 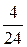 =
= 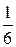 = 0.17.
= 0.17.
2. Четыре человека, среди которых двое знакомых, случайным образом рассаживаются в ряд, состоящий из шести стульев. Какова вероятность того, что знакомые окажутся рядом сидящими?
n =  , m = (4∙2 + 2) ∙
, m = (4∙2 + 2) ∙ 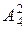 =
= 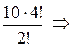 P =
P = 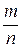 =
= 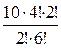
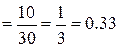 . 3. Из группы, состоящей из 4 студенток и 7 студентов, случайным образом отбираются 5 человек. Какова вероятность того, что среди отобранных окажется ровно 2 студентки?
. 3. Из группы, состоящей из 4 студенток и 7 студентов, случайным образом отбираются 5 человек. Какова вероятность того, что среди отобранных окажется ровно 2 студентки?
 ,
, 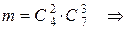
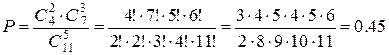 .
.
4. Из урны, в которой находятся 5 красных, 2 синих и 4 желтых шара наудачу без возвращения в урну извлекаются:
1. 7 шаров. Найти вероятность того, что среди этих шаров окажется ровно 3 красных;
2. 2 шара. Найти вероятность того, что:
а) это будут желтые шары;
б) эти шары будут одного цвета;
в) эти шары будут разного цвета;
г) среди этих шаров будут хотя бы один красный;
3. 3 шара. Найти вероятность того, что:
а) эти шары будут одного цвета;
б) эти шары будут разных цветов;
в) взятый из них наудачу один шар окажется желтым;
4. 2 шара и они оказались одного цвета. Найти вероятность того, что это красные шары.
Решение.
1. В урне 5 красных и 6 некрасных шаров
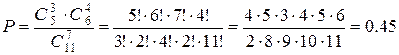 .
.
2. a) P(ж и ж) = 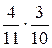 = 0.11.
= 0.11.
б) P(к и к или с и с или ж и ж) = 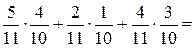
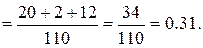
в) Для двух шаров событие «шары разного цвета» противоположно
событию «шары одного цвета» => P(в) = 1 − P(б) = 1 – 0.31 = 0.69.
г) Считаем, что в урне 5 красных и 6 некрасных шаров и найдем
P(A) = 1 – P( 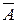 ) = 1 – P(н и н) =
) = 1 – P(н и н) = 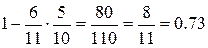 .
.
3. а) Р(к и к и к или с и с и с или ж и ж и ж) = 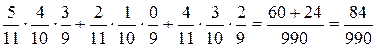 = 0.085.
= 0.085.
б) P(к, ж, с) = 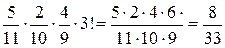 = 0.24
= 0.24
Примечание. Множитель 3! Соответствует числу перестановок 3-х элементов.
в) Решим задачу по формуле полной вероятности. В урне находятся 4 желтых и 7 нежелтых шаров. Событие А – желтый шар из 3-х.
Гипотезы: H1 – 3 желтых шара;
H2 – 2 желтых и 1 нежелтый;
H3 − 1 желтый и 2 нежелтых;
H4 – 3 нежелтых.
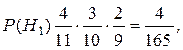
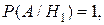
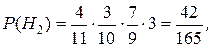
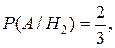
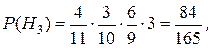
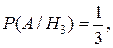
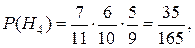
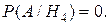
Контроль 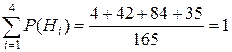
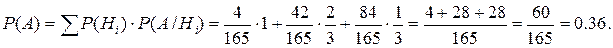
4. Считаем, что в урне 5 красных и 6 некрасных шаров. Событие А – шары одного цвета.
Гипотезы:
Н1 – 2 красных шара;
Н2 – 2 некрасных шара;
Н3 – 1 красный и 1 некрасный.
Надо найти 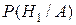 . По формуле Байеса
. По формуле Байеса 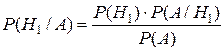 .
.
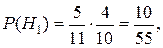
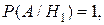
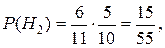
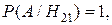

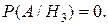
Контроль 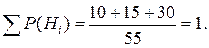
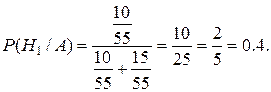
5. В урне находятся 5 красных и 8 синих шаров. Шар извлекается и возвращается в урну 4 раза. Найти вероятность того, что красный шар появится:
а) ровно 3 раза; б) не менее 2-х раз.
Для решения задачи применяем формулу Бернулли 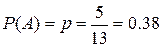 ,
, 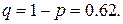
а) 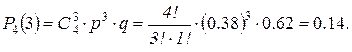
б) 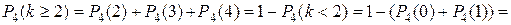
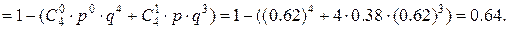
6. Из урны, содержащей 7 синих и 8 желтых шаров наудачу извлекаются 4 шара. Построить ряд распределения и найти математическое ожидание случайной величины равной числу синих шаров среди извлеченных 4-х шаров.
Значение случайной величины 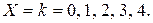
Найдем их вероятности:
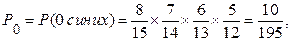
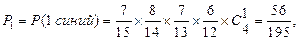
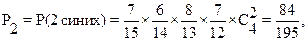
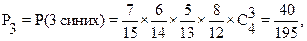
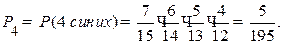
Проверим свойство ряда: 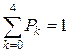 .
.
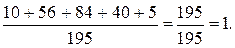
| Xk | |||||
| Pk | 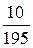
| 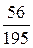
| 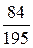
| 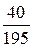
| 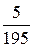
|
Итак, ряд распределения Х :
Математическое ожидание
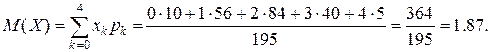
7. Дискретная случайная величина Х с известным математическим ожиданием М(Х) = 3.7 задана рядом распределения:
| Xi | 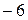
| 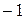
| |||
| Pi | 0.1 | р2 | 0.2 | р4 | 0.2 |
Требуется:
а) найти p2 и p4;
б) построить многоугольник распределения;
в) построить интегральную функцию F(x) и ее график;
г) вычислить дисперсию и среднее квадратическое отклонение.
Решение:
а) найдем из условий 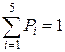 и
и 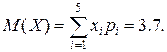
Получим систему уравнений:
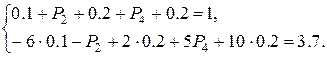
| Xi | − 6 | − 1 | |||
| Pi | 0.1 | 0.1 | 0.2 | 0.4 | 0.2 |
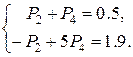
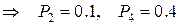 .
.
б) для ряда распределения:
строим многоугольник распределения:
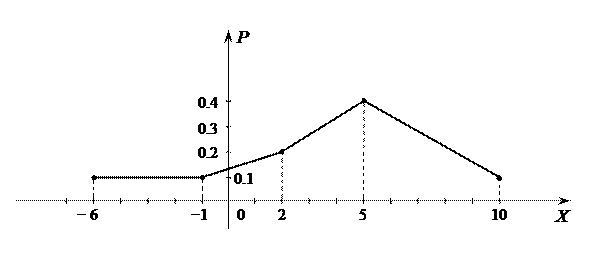
в) интегральную функцию 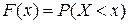 строим с помощью свойства
строим с помощью свойства 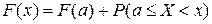 :
:
при 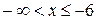
| 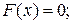
|
при 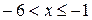
| 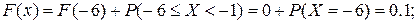
|
при 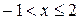
| 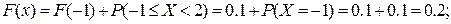
|
при 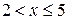
| 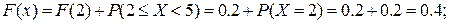
|
при 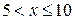
| 
|
при 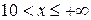
| 
|
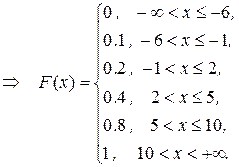
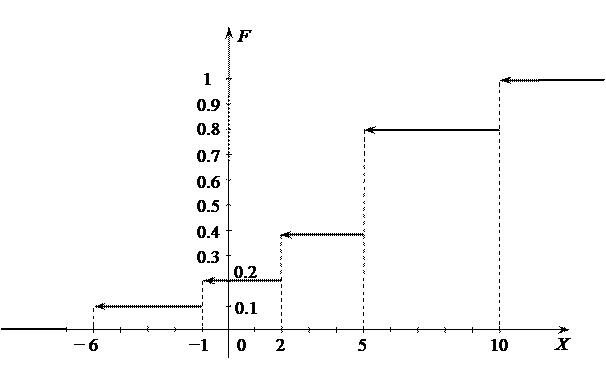
г) дисперсия  .
.
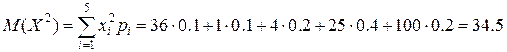
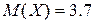 (по условию)
(по условию) 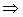
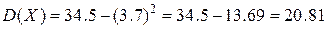 и
и
среднее квадратическое отклонение 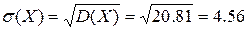 .
.
8. Задана дифференциальная функция (плотность) распределения
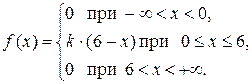
Найти:
а) параметр 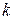 ;
;
б) интегральную функцию 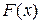 ;
;
в) математическое ожидание 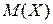 и дисперсию
и дисперсию 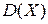 ;
;
г) вероятность события 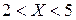 .
.
Решение:
а) из условия 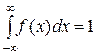
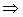
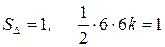
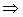
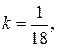
тогда 



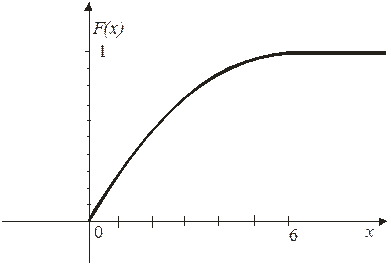
б) 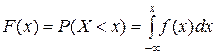
При построении 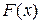 воспользуемся свойством
воспользуемся свойством
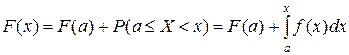 .
.
При 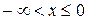
| 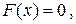
|
при 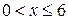
| 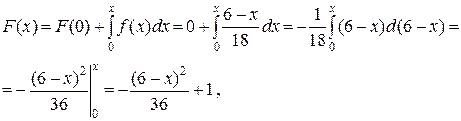
|
при 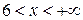
|  . .
|
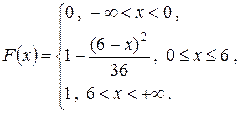



в) 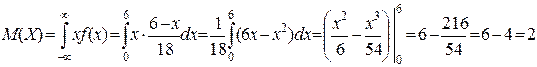 .
.
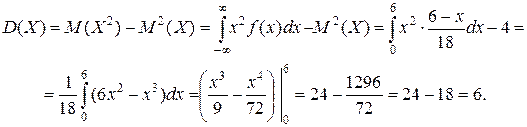
г) 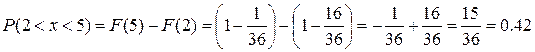 .
.
9. На запуск двигателя тратится в среднем 2.5 попытки. Считая, что вероятность запуска в каждой попытке одинакова, найти вероятность запуска двигателя не более, чем за 3 попытки.
Здесь имеет место геометрическое распределение случайной величины Х равной числу попыток до запуска двигателя, причем 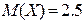 . Тогда из
. Тогда из 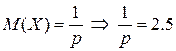 и
и 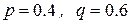 .
.

10. Случайная величина Х имеет биномиальное распределение (распределение Бернулли) с математическим ожиданием 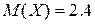 и дисперсией
и дисперсией 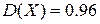 . Найти вероятность события
. Найти вероятность события 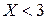 .
.
Для биномиального распределения 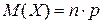 ,
, 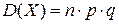
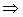
получим систему уравнений:

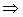
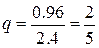 , тогда
, тогда 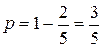 и
и 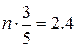
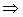
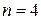 .
.
Искомую вероятность 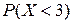 находим с помощью формулы Бернулли.
находим с помощью формулы Бернулли.
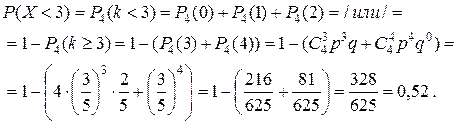
11. Для случайной величины Х, имеющей распределение Пуассона вероятность события  равна 0.4. Найти вероятность события
равна 0.4. Найти вероятность события 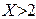 .
.
Из формулы 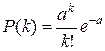 для
для 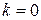
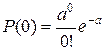 ,
, 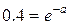
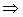
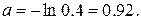
Тогда 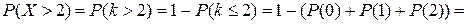
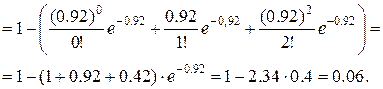
12. Случайная величина Х имеет равномерное распределение в интервале 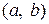 , причем
, причем 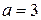 и
и 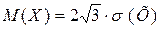 . Найти вероятность события
. Найти вероятность события 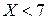 .
.
Для равномерного распределения 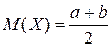 ,
, 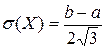 .
.
По условию 
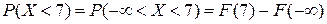 . Для
. Для 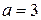 и
и 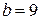 интегральная функция имеет вид:
интегральная функция имеет вид:

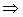
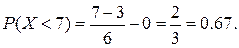
13. Случайная величина Х имеет показательное распределение и при этом численно 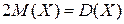 . Найти вероятность события
. Найти вероятность события 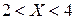 .
.
Из формул 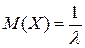 ,
, 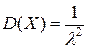
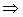
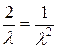 или
или 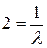 .
.
Тогда 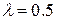 и интегральная функция будет:
и интегральная функция будет:
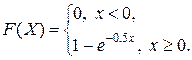
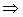
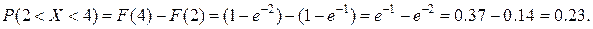
14. Методами математической статистики установлено, что для данного региона роста призывников в ряды вооруженных сил имеют нормальное распределение с параметрами 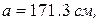
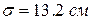 . Найти ожидаемое число призывников 3-го роста из 1000 человек.
. Найти ожидаемое число призывников 3-го роста из 1000 человек.
Отметим, что третий рост соответствует интервалу (167, 173).
По формуле 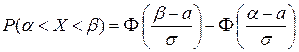 получим
получим

Тогда ожидаемое число призывников третьего роста
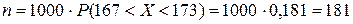 человек.
человек.
Примечание: значения 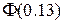 и
и 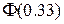 взяты из таблицы значений функции Лапласа
взяты из таблицы значений функции Лапласа 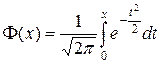 .
.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Для получения своих личных данных надо подставить α и β в задания и посчитать соответствующие им выражения.
α – предпоследняя, а β – последняя цифра шифра студента.
Например, если шифр студента 1004-206, то α=0, β=6.
1 Из урны, в которой находятся (12-β) белых, (2+α) черных и 3 синих шара наудачу, без возвращения в урну извлекаются:
1) 5 шаров. Найти вероятность того, что среди этих шаров окажется ровно два белых.
2) 2 шара. Найти вероятность того что:
а) эти шары будут разного цвета;
б) эти шары будут одного цвета;
в) взятый из них наудачу один шар окажется белым.
3) 3 шара. Найти вероятность того, что:
а) эти шары будут разного цвета;
б) эти шары буду одного цвета;
в) среди этих шаров будет хотя бы один белый.
4) 2 шара, и они оказались разного цвета. Найти вероятность того, что это белый и черный шары.
2 В урне находятся (5+β) белых и (15-β) черных шаров. Наудачу, шар извлекается и возвращается в урну 3 раза. Найти вероятность того, что белый шар появится:
а) ровно 2 раза;
б) не менее одного раза.
3 В урне находятся (12-β) белых и (12-α) черных шаров. Наудачу извлекаются без возвращения в урну 3 шара. Построить ряд распределения и найти математическое ожидание случайной величины, равной числу белых шаров среди извлеченных трех шаров.
4 Дискретная случайная величина Х с математическим ожиданием М(Х)=6+0,1α-0,3β задана рядом распределения
| xi | α-10 | 10-β | ||
| pi | p1 | 0,4 | p3 | 0,2 |
а) Найти р1 и р3;
б) построить многоугольник распределения;
в) построить интегральную функцию распределения F(x) и её график;
г) вычислить дисперсию D(x).
5 Плотность распределения непрерывной случайной величины X имеет вид
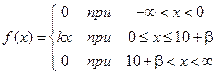
Найти: а) параметр k;
б) математическое ожидание М(х);
в) интегральную функцию распределения F(x) и её график;
г) вероятность события X >10-α.
6 Случайная величина имеет биноминальное распределение с математическим ожиданием M(x)= 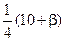 и дисперсией D(x)=
и дисперсией D(x)= 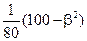 . Найти вероятность события X ³ 2.
. Найти вероятность события X ³ 2.
7 Случайная величина имеет нормальное распределение с математическим ожиданием M(x)= 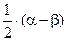 и дисперсией D(x)=
и дисперсией D(x)= 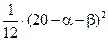 . Найти вероятность события X >0.
. Найти вероятность события X >0.
| <== предыдущая страница | | | следующая страница ==> |
| Модуль гамма–каротажа (ГК) в процессе бурения | | | ЗДРАВООХРАНЕНИЕ В УСЛОВИЯХ РЫНКА |
Дата добавления: 2014-11-24; просмотров: 1040; Нарушение авторских прав

Мы поможем в написании ваших работ!