Сингулярные функции

1. Под регулярной (гладкой) функцией y = f(x) понимают однозначное соответствие между множествами значений y и значений x.

2. Сингулярными принято называть функции, у которых нарушается однозначность соответствия значений y и x. К простейшим сингулярным функциям относятся единичная функция 1(t) и дельта-функция d(t).

3. Сингулярную функцию всегда можно определить как предел последовательности гладких функций при стремлении некоторого параметра к нулю. В связи с этим они допускают операции дифференцирования и интегрирования.

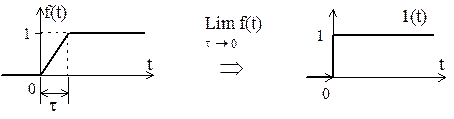
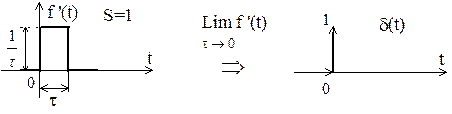
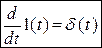Þ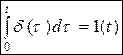

4. Записи 1(t-t₁) и d(t-t₁) соответствует сдвиг сингулярных функций по времени на t_1.

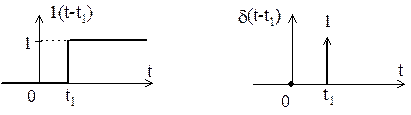
5. Величина 1(t-t₁) и площадь d(t₁) - безразмерные величины, поэтому при описании воздействий эти функции следует умножать на коэффициенты, имеющие размерность (В, мВ, мкВ и т.д.).

Дата добавления: 2014-11-24; просмотров: 205; Нарушение авторских прав

Мы поможем в написании ваших работ!