
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Первый замечательный предел
Пример 4.1. Вычислить 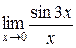 .
.
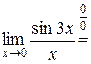
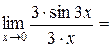
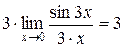 , так как
, так как 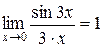 .
.
Этот же пример можно было решить, используя таблицу эквивалентных б.м. функций: 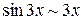 при
при 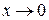 . Тогда
. Тогда 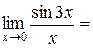
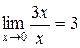 .
.
Пример 4.2. Вычислить 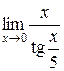 .
.
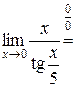
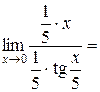
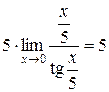 , так как
, так как 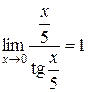 , или с использованием эквивалентности
, или с использованием эквивалентности 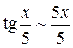 при
при 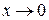 :
: 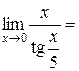
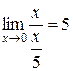 .
.
Пример 4.3. Вычислить 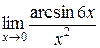 .
.
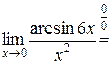
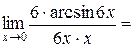
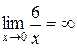 , так как числитель – константа, а знаменатель – б.м. функция.
, так как числитель – константа, а знаменатель – б.м. функция.
Пример 4.4. Вычислить 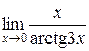 .
.
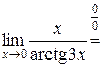
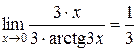 , так как
, так как 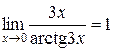 .
.
В примерах 4.3, 4.4 тоже можно было воспользоваться таблицей эквивалентных б.м. функций. Предлагаем читателю сделать это самостоятельно.
Пример 4.5. Вычислить 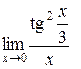 .
.
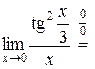
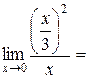
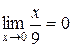 .
.
Воспользовались отношением 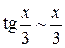 , а, следовательно,
, а, следовательно, 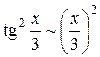 при
при 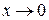 .
.
Пример 4.6. Вычислить 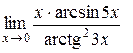 .
.
Так как 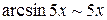 ,
, 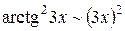 при
при 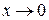 , то
, то
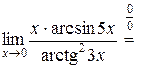
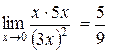 .
.
Пример 4.7. Найти 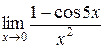 .
.
В числителе воспользуемся формулой 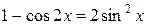 . Так как
. Так как 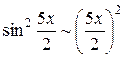 при
при 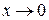 , то получим
, то получим
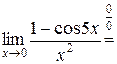
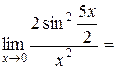
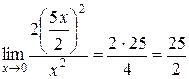 .
.
Пример 4.8. Найти 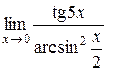 .
.
Имеем 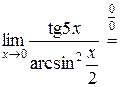

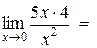
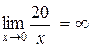 , так как
, так как
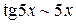 ,
, 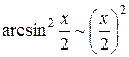 при
при 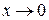 .
.
Пример 4.9. Найти 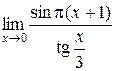 .
.
Нельзя сразу воспользоваться таблицей эквивалентных б.м. функций для 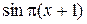 , так как
, так как 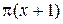 не является б.м. функцией при
не является б.м. функцией при 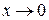 . Поэтому сначала применим формулу приведения
. Поэтому сначала применим формулу приведения 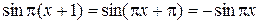 . Далее, так как
. Далее, так как 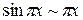 ,
, 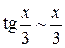 при
при 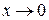 , то
, то 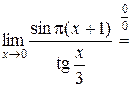
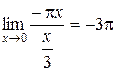 .
.
Пример 4.10. Найти 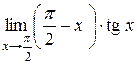 .
.
Выполним замену переменной, обозначив 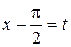 , тогда
, тогда 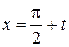 и при
и при 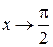 ,
, 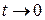 . Поэтому
. Поэтому
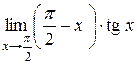
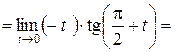
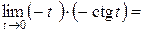
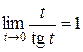 .
.
Воспользовались формулой приведения 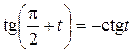 и формулой
и формулой 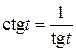 .
.
Пример 4.11. Найти 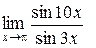 .
.
Сделаем замену переменной 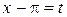 , тогда
, тогда  и при
и при 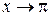
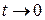 . Имеем
. Имеем
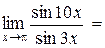
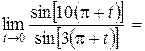
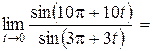
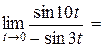
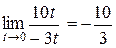 .
.
Применили формулы 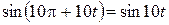 ,
, 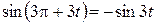
и отношения эквивалентности 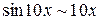 ,
, 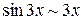 при
при 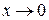 .
.
Пример 4.12. Найти 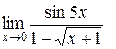 .
.
Так как 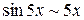 при
при 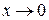 , то имеем
, то имеем
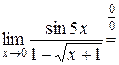
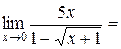
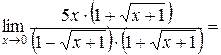
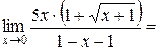
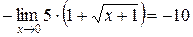 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление пределов, содержащих иррациональность | | | Второй замечательный предел |
Дата добавления: 2014-02-28; просмотров: 746; Нарушение авторских прав

Мы поможем в написании ваших работ!