Способ, основанный на зависимости между геодезическими и плоскими прямоугольными координатами

Аналитические способы преобразования плоских прямоугольных координат

Этот способ состоит в том, что, имея плоские прямоугольные координаты (x₁;y₁) точки в одной зоне вычисляются её геодезические координаты (B;L). Затем с учётом разности долгот осевых меридианов соответствующих зон, используя найденные геодезические координаты (В; L′), вновь определяют плоские прямоугольные координаты (X₂;y₂) точки, но в смежной зоне.

Для 6⁰-градусной зоне L′=L±6⁰, значение широты в соответствии с проекцией Гаусса не изменяется. В этих случаях для описания положения точек берут системных координат обеих смежных зон. Упрощенные формулы перехода от геодезических координат точки к плоским прямоугольным координатам имеют вид:

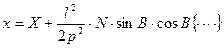
Значение величин входящих в эти формулы можно показать следующим рисунком (рис. 2.2).

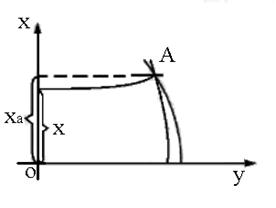
Рис. 2.2. Зависимость геодезических и плоских прямоугольных координат точки

Х- длина дуги меридиана от экватора до параллели данной точки; N- радиус кривизны поверхности эллипсоида; p- значение радиана; l=L-L₀-

разность долгот меридиана данной точки и осевого меридиана зоны; В- геодезическая широта точки.

Для преобразования плоских прямоугольных координат из одной 6- градусной зоны в другую могут применяться различные таблицы, в которых даны рекомендации по их применению.

Способ преобразования координат по двум связующим точкам.

Для применения данного способа две или более точки должны иметь координаты в одной и другой системе координат. Такие точки называются связующими. Этот способ чаще всего применяется для преобразования координат из одной местной системы координат в другую.

В основу способа положен перенос начала отсчёта координат одной системы (точка О₁) в начало отсчёта другой системы (точка О₂) с одновременным разворотом второй относительно первый на угол Q (рис.2 .3)

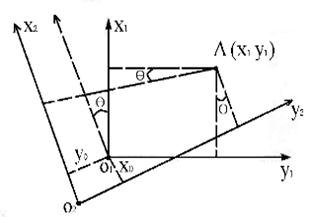
Рис. 2.3. Схема положения точки в разных системах координат

Схема положения точки в разных системах координат. Такая задача решается в аналитической геометрии по следующим формулам:

x₂=x₀+x₁ cosQ- y₁sin Q;

y=y₀+y₁ cos Q+X₁ sin Q;

где x₀ и y₀ координата начала отсчёта новой системы координат;

х₁; y₁, x₂, y₂- координаты точки в старой и новой системах координат; Q- угол поворота осей координат.

Задача по преобразованию координат из одной местной системы в другую может быть такой: имеются координаты n- точек в системе координат одной зоны, требуется определить координаты этих точек в системе координат другой зоны. Из всех n- точек две точки, например А и В которые являются связующими имеют координаты в одной и другой системах координат.

Тогда, решив две обратные геодезические задачи для точек А и В по координатам одной и другой системы координат получают два дирекционных угла (α_ав и α_ав′) и два горизонтальных проложения (S_ав и S_а′в). Затем вычисляют угол поворота осей координат Ө, масштабный множитель m и коэффициенты К₁, К₂ по формулам:

Ө=α_а′в-α_ав,

m=

К₁=m cosӨ, К₂=m sinӨ.

Коэффициенты К₁ и К₂ являются значениями поправок в приращения координат за преобразование координат точек из одной системы координат в другую. Используя эти коэффициенты определяют координаты других (n-2)точек.

Преобразуются так для следующей после точки в координаты точки С будут.

Xc′=X_B′+(x_c-x_B)K₁- (y_c-y_в) К₂;

y_c′=y_в′+(y_c-y_в)к₁+ (х_с-х_в)к₂.

В этих формулах Х_в, y_в; х_с, y_с координаты точки В и св системе координат исходной зоны, а х_в′ y_в′; х_с; y_c′ преобразованные координаты этих точек.

Таким же образом осуществляется преобразование координат последующих точек.

Лекция 3

Дата добавления: 2014-02-28; просмотров: 866; Нарушение авторских прав

Мы поможем в написании ваших работ!