Улучшение аппроксимации

Как видно из конечно-разностных соотношений для аппроксимаций производ­ных , порядок их точности прямо пропорциона­лен числу узлов, используемых при аппроксимации. Од­нако с увеличением числа узлов эти соотношения стано­вятся более громоздкими, что приводит к существенному возрастанию объема вычислений. Усложняется также оценка точности получаемых результатов. Вместе с тем существует простой и эффективный способ уточнения ре­шения при фиксированном числе узлов, используемых в аппроксимирующих конечно-разностных соотношениях. Это метод Рунге Ромберга. Изложим вкратце его сущность.

Пусть 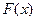- производная, которая подлежит аппрок­симации; - конечно-разностная аппроксимация этой производной на равномерной сетке с шагом - погрешность (остаточный член) аппроксимации, главный член которой можно записать в виде , т. е.

.

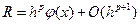Тогда выражение для аппроксимации производной в об­щем случае можно представить в виде

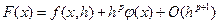(16).

Запишем это соотношение в той же точке 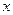при другом шаге 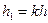. Получим

(17).

Приравнивая правые части равенств (16) и (17), на­ходим выражение для главного члена погрешности аппроксимации производной:

.

Подставляя найденное выражение в равенство (16), получаем формулу Рунге:

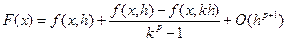(18).

Эта формула позволяет по результатам двух расчетов значений производной и 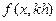(с шагам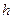и и 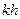) с порядком точности найти ее уточненное значение с порядком точности .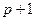

Таким образом, формула Рунге дает более точное значение производной. В общем случае порядок точности ап­проксимации увеличивается на единицу.

Мы рассмотрели уточнение решения, полученного при двух значениях шага. Предположим теперь, что расчеты могут быть проведены с шагами . Тогда можно получить уточненное решение для производной 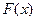по формуле Ромберга, которая имеет вид

Таким образом, порядок точности возрастает на . Заметим, что для успешного применения уточнения ис­ходная функция должна иметь непрерывные производные достаточно высокого порядка.

Дата добавления: 2014-03-01; просмотров: 489; Нарушение авторских прав

Мы поможем в написании ваших работ!