Частные производные. Рассмотрим функцию двух переменных , заданную в табличном виде: , где

Рассмотрим функцию двух переменных 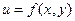, заданную в табличном виде: , где . В таблице 2 представлена часть дан­ных, которые нам в дальнейшем понадобятся.

Используя понятие частной производной, можем при­ближенно записать для малых значений шагов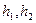

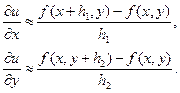
Воспользовавшись введенными выше обозначениями, получим следующие приближенные выражения (аппроксимацию) для частных производных в узле 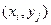с по­мощью отношений конечных разностей:

Для численного дифференцирования функций многих переменных можно, как и ранее, использовать интерпо­ляционные многочлены.

Таблица 2.

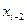
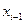
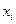
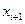
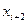
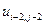
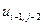
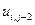
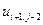
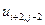
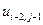
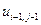
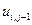
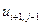
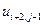
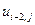
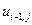
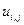
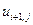
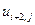
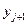
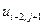
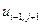
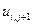
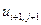
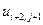
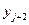
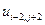
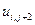
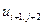
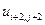
Однако рассмотрим здесь другой способ – разложение в ряд Тейлора функции двух переменных:

(19).

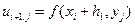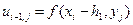Используя эту формулу дважды: нейдем при ; нейдем при 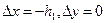. Получим

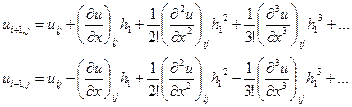
Вычитая почленно из первого равенства второе, получаем

.

Отсюда найдем аппроксимацию производной с помощью центральных разностей:

.

Она имеет второй порядок.

Аналогично могут быть получены аппроксимации производной , а также старших производных. В частности, для второй производной можно получит

.

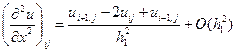Записывая разложения в ряд (19) при разных зна­чениях и 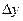, можно вывести формулы численного дифференцирования с необходимым порядком аппрок­симации.

Приведем окончательные формулы для некоторых ап­проксимаций частных производных. Слева указывается комбинация используемых узлов (шаблон), которые от­мечены кружочками. Значения производных вычисляются в узле (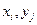), отмеченном крестиком (напомним, что на шаблонах и в табл. 2 по горизонтали изменяются пере­менная 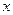и индекс 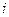, по вертикали - переменная 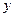и индекс ):

,

,

,

,

,

,

,

,

,

,

.

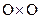
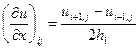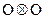
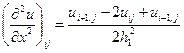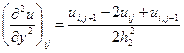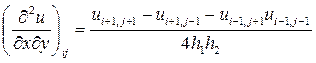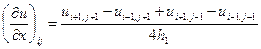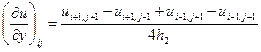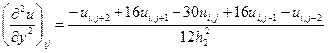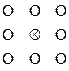
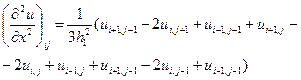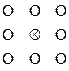
Приведенные аппроксимации производных могут быть использованы при построении разностных схем для ре­шения уравнений с частными производными.

Дата добавления: 2014-03-01; просмотров: 598; Нарушение авторских прав

Мы поможем в написании ваших работ!