Имитационное моделирование

Имитационная модель представляет собой формализованное описание экономической системы через ее элементы и зависимости между ними, порядок расчета показателей, характеризующих эти элементы и зависимости, представленный в виде алгоритма, реализуемого на ЭВМ с помощью специальных программ. Расчеты имеют своей целью получение знаний об особенностях функционирования моделируемого объекта. Сложность моделируемых систем обусловила выделение в ней отдельных составляющих и формализованное описание или с помощью ранее разработанных аналитических моделей или вновь создаваемых с последующей их интеграцией в единую имитационную модель. Прибегать к имитационному моделированию целесообразно в тех случаях, когда отсутствуют или не могут быть использованы разработанные аналитические методы решения проблемы, имеется полная уверенность в успешном создании модели, имеется возможность получения достаточного количества экспериментальных расчетов с помощью данной модели.

Одно из важнейших свойств имитационной модели – возможность воспроизведения действия системы и выявление влияния случайных факторов.

Обычно при разработке модели функционирования экономической системы выделяют следующие типы взаимосвязей и ограничений:

1. Балансовые отношения и отношения потоков

а) балансовые потоки в физическом измерении

б) балансовые отношения для стоимостных показателей

в) отношения, характеризующие равенство стоимостей объемам, умноженным на цены

г) уравнения, определяющие индексы

д) соотношения финансовых потоков.

2. Технологические отношения производства

а) взаимосвязи, характеризующие производственные возможности в краткосрочном периоде

б) соотношения, характеризующие влияние инвестиций в новое оборудование на производственные мощности.

3. Поведенческие отношения

а) поведение производителей

б) поведение потребителей

в) поведение в финансовом секторе

г) отношения внешней торговли.

4. Организационные (институциональные) соотношения

а) налогообложения

б) социального страхования

в) взаимосвязи между разными уровнями государственного сектора

г) условия функционирования финансовых институтов

д) процессы ценообразования

е) принципы оценки фондов материального стимулирования

ж) системы нормирования и лицензирования

з) соотношения рыночного равновесия.

5. Демографические, биологические и экологические соотношения.

6. Прогнозы неконтролируемых экзогенных переменных.

7. Отношения предпочтения

а) функция предпочтения

б) ограничение предпочтения

в) социальные индикаторы.

Для рыночной экономики характерны поведенческие взаимосвязи и отношения, связанные с описанием неконтролируемых экзогенных переменных. Для краткосрочного периода модели должны включать все типы соотношений, за исключением отношений предпочтения, так как они заменяются фиксированными целевыми показателями. Для долгосрочного периода в модель включают в основном балансовые, технологические, демографические, биологические и экологические соотношения.

В имитационном моделировании широко используется теория игр – раздел прикладной математики с помощью которого устанавливают оптимальную стратегию поведения субъекта в конфликтных ситуаций, под которыми понимают ситуацию столкновения интересов двух или более сторон, преследующих различные цели. Каждый из участников конфликта может оказывать некоторое влияние на ход событий, но не имеет возможности полностью им управлять.

Математическая модель должна описать:

- множество заинтересованных сторон;

- возможные действия каждой стороны

- интересы сторон, представленные функциями выигрыша для каждого из игроков.

В теории игр предполагается, что функции выигрыша и множество стратегий, доступных каждому из игроков, общеизвестны.

Игры классифицируются, основываясь на том или ином принципе.

- По числу игроков (2,3 и т.д. игрока)

- По количеству стратегий

· конечные

· бесконечные

- По свойствам функций:

· игры с нулевой суммой (выигрыш одного игрока равен проигрышу другого)

· игры с постоянной разностью (игроки и выигрывают и проигрывают одновременно, так что им выгодно действовать сообща)

· игры с ненулевой суммой (имеются и конфликты и согласованные действия)

- По возможности предварительных переговоров между игроками

· кооперативные

· некооперативные.

В экономических задачах количество вариантов велико и поэтому выбрать оптимальный вариант сложно. В теории массового обслуживания для этого используется теория очереди.

В данном случае предполагается, что заявки на элементарные операции приходят в случайные моменты времени и обслуживаются в течение случайных промежутков времени. Поэтому необходимо изучить статистику поступления заявок и сроков их выполнения и разработать модель данного процесса.

Метод Монте-Карло - имитация массового процесса путем вычисления его хода, в котором случайные колебания определяются с помощью жребия или таблицы случайных чисел. Распределение вероятностей может задаваться в виде формул, таблиц, кривых.

Если имеется модель парной регрессии, в которой y связан с х следующей зависимостью:

Y =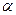+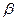x + u

То можно использовать метод Монте-Карло следующим образом:

1) Выбирают истинные значения 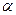и 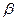, в каждом наблюдении выбирается значение х и используется некоторый процесс генерации случайных чисел для получения случайного фактора u в каждом из наблюдений.

2) В каждом наблюдении генерируется значение Y, используя значения 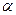, , 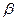х, u.

3) Применяется регрессионный анализ для оценивания параметров уравнения регрессии

Y = a + bx с использованием только полученных указанным образом значений Y и данных для х. При этом можно определить насколько хорошими оценками для 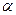и 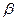являются а и b.

Данный метод применяется в расчетах для сложных комплексов, в которых использование классических методов вычисления практически невозможно (управление запасами, системы массового обслуживания и т.д.).

Дата добавления: 2014-03-01; просмотров: 462; Нарушение авторских прав

Мы поможем в написании ваших работ!