Метод наименьших квадратов

Поиск локальных экстремумов функции двух переменных активно применяется в задаче о проведении прямой линии, наиболее близкой к n заданным точкам на плоскости. Известно, что через одну точку можно провести бесчисленное множество прямых, через две точки – единственную прямую. Через произвольные 3 точки прямую провести нельзя. Тем более, через 5 точек. Но представим, что проведены замеры в 5 точках (x=1, x=2, x=3, x=4, x=5). Значения, полученные при замерах, соответственно, равны: y=1, y=1, y=2, y=5, y=6.

Нанесем результаты наблюдений на плоскость. Мы видим, что если соединить точки последовательно, полученная линия будет близка к прямой.

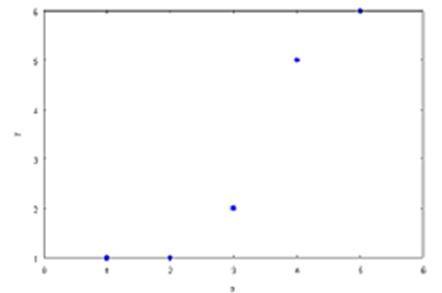
Учитывая, что замеры производятся неточно, мы хотим нарисовать приближенный график линейной зависимости 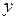от 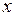. Не существует прямой, проходящей через пять полученных на плоскости точек, но можно постараться провести прямую максимально близко к полученным точкам.

Уравнение прямой на плоскости 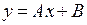зависит от двух параметров A и B. Нужно подобрать их так, чтобы при значениях x, равных 1, 2, 3, 4 и 5, значения 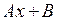мало отличались от 1, 1, 2, 5 и 6, соответственно. Это значит, что нужно подобрать такие A и B, чтобы значение функции

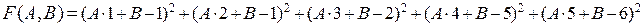было минимальным. Это значит, должно выполняться необходимое условие экстремума: 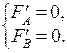В данном случае после приведения подобных членов получим 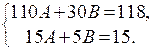Решая эту систему, найдем 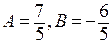. Исследовав знак второго дифференциала, увидим, что он положителен, следовательно, в данной точке функция 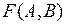имеет минимум.

Таким образом, уравнение искомой прямой: .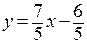

Нарисуем график с помощью MAXIMы: введем xy: [[1, 1], [2, 1], [3, 2], [4, 5], [5, 6]]; plot2d([[discrete, xy], 7/5*x-6/5], [x,0,6],[style, points, lines]); и нажмем Shift+Enter. Получим

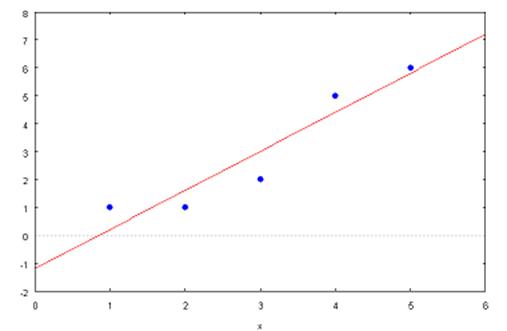
Предложенный метод нахождения прямой, проходящей наиболее близко к заданным точкам, называется методом наименьших квадратов.

Заметим, что пакет программ MAXIMA содержит этот метод. Для того, чтобы решить ту же задачу при помощи компьютера, следует сначала ввести координаты точек на плоскости: записать load (lsquares);

M : matrix ( [1,1], [2,1], [3,2], [4,5], [5,6])и нажать Shift+Enter.

Компьютер выведет на экран и запомнит 5 заданных точек в виде матрицы из двух столбцов. Затем введем команды lsquares_estimates (M, [x,y], y = A*x+B, [A,B])и нажмемShift+Enter. Компьютер выведет на экран ответ 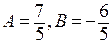, который мы уже получили выше.

Тот же метод наименьших квадратов можно применять, проводя вблизи заданных точек кривые требуемого вида на плоскости или поверхности в пространстве при условии, что количество заданных точек превышает количество параметров в интересующей нас кривой или поверхности.

Дата добавления: 2014-03-03; просмотров: 741; Нарушение авторских прав

Мы поможем в написании ваших работ!