Локальный экстремум в случае функции трех и более числа переменных

В том случае, когда следует найти локальные экстремумы функции 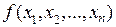, следует сначала отыскать все критические точки функции, решив систему из 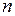уравнений с 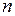переменными: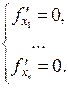

Для того, чтобы выяснить, будет ли критическая точка 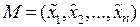точкой локального экстремума, следует выяснить, будет ли сохраняться знак 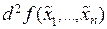вне зависимости от наборов бесконечно малых приращений 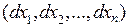. Легко заметить, что дифференциал второго порядка представляет собой квадратичную форму относительно этих бесконечно малых приращений. Поэтому вопрос о сохранении знака этого дифференциала сводится к вопросу о сохранении знака соответствующей квадратичной формы.

Таким образом, для исследования вопроса о том, будет ли критическая точка точкой экстремума, следует сосчитать в этой точке все частные производные второго порядка, составить матрицу вида 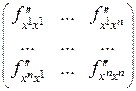и рассмотреть последовательность определителей, состоящих из элементов в левом верхнем углу матрицы: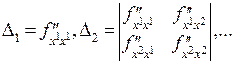

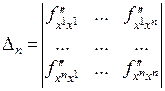. Минимум в критической точке 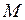будет тогда и только тогда, когда 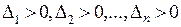. Максимум в критической точке 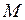будет тогда и только тогда, когда 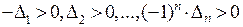, то есть, знаки у последовательности определителей обязаны чередоваться.

Дата добавления: 2014-03-03; просмотров: 369; Нарушение авторских прав

Мы поможем в написании ваших работ!