
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Необходимое условие локального экстремума
Локальный экстремум функции многих переменных.
Точкой локального экстремума функции 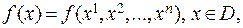 называется такая точка
называется такая точка , для которой в области
, для которой в области 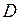 существует окрестность, в которой разность
существует окрестность, в которой разность 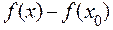 не меняет знак. В частности, точка
не меняет знак. В частности, точка 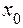 является точкой минимума, если
является точкой минимума, если 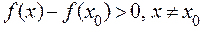 , и точка
, и точка 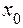 является точкой максимума, если
является точкой максимума, если 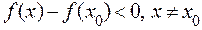 .
.
Пусть 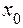 – точка экстремума, и функция
– точка экстремума, и функция 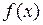 дифференцируема в точке
дифференцируема в точке 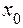 . Рассмотрим функцию одной переменной
. Рассмотрим функцию одной переменной 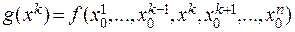 , где
, где 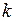 – любое натуральное число между 1 и
– любое натуральное число между 1 и 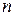 . Эта функция имеет точкой экстремума точку
. Эта функция имеет точкой экстремума точку 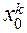 , и значит,
, и значит, 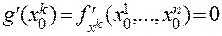 . Следовательно, необходимым условием экстремума функции многих переменных
. Следовательно, необходимым условием экстремума функции многих переменных 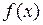 в точке
в точке 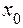 , где она дифференцируема, является следующее условие:
, где она дифференцируема, является следующее условие: 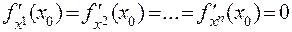 . Точка, в которой все частные производные первого порядка данной функции равны нулю, называется критической точкой этой функции.
. Точка, в которой все частные производные первого порядка данной функции равны нулю, называется критической точкой этой функции.
Достаточное условие локального экстремума.
Выполнение необходимого условия экстремума не обязательно обеспечивает действительное наличие экстремума в точке, то есть, критическая точка функции может не быть точкой локального экстремума. В качестве примера рассмотрим функцию двух переменных 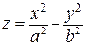 . Критической точкой для этой функции является точка (0,0). Однако эта точка является не экстремальной, а седловой.
. Критической точкой для этой функции является точка (0,0). Однако эта точка является не экстремальной, а седловой.
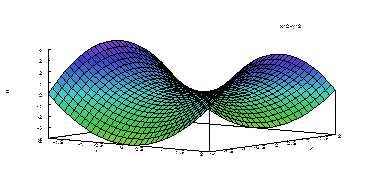
Для того чтобы выяснить, достигается ли в критической точке экстремум и какой, следует обратиться к дифференциалу второго порядка в этой точке. Итак, пусть 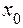 – критическая точка для функции многих переменных
– критическая точка для функции многих переменных 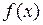 . В этом случае
. В этом случае 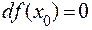 . В соответствии с формулой Тейлора
. В соответствии с формулой Тейлора
 где
где 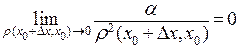 .
.
Поэтому знак разности 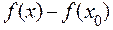 в окрестности точки
в окрестности точки 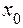 определяется знаком дифференциала второго порядка в точке
определяется знаком дифференциала второго порядка в точке 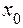 при всевозможных малых приращениях
при всевозможных малых приращениях 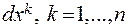 .
.
Второй дифференциал функции в точке представляет собой квадратичную форму относительно переменных 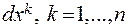 . Поэтому исследование вопроса о наличии экстремума сводится к исследованию вопроса о сохранении знака квадратичной формы, а значит, к вычислению угловых миноров соответствующей матрицы из коэффициентов.
. Поэтому исследование вопроса о наличии экстремума сводится к исследованию вопроса о сохранении знака квадратичной формы, а значит, к вычислению угловых миноров соответствующей матрицы из коэффициентов.
Рассмотрим случай 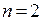 . Пусть критическая точка имеет координаты
. Пусть критическая точка имеет координаты 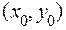 . Рассмотрим приращение функции в окрестности этой точки:
. Рассмотрим приращение функции в окрестности этой точки: 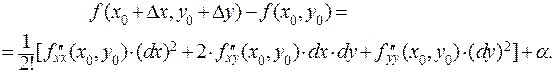
Если при любом сочетании бесконечно малых приращений 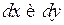 выражение в квадратных скобках не меняет знак, то данная критическая точка является точкой локального экстремума. Вынесем за квадратную скобку множитель
выражение в квадратных скобках не меняет знак, то данная критическая точка является точкой локального экстремума. Вынесем за квадратную скобку множитель 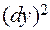 . Знак приращения функции совпадает со знаком квадратного трехчлена
. Знак приращения функции совпадает со знаком квадратного трехчлена 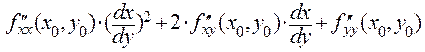
относительно 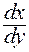 . Как известно, квадратный трехчлен не меняет знак в том случае, если не имеет корней, то есть если его дискриминант отрицателен. В случае отрицательного дискриминанта знак квадратного трехчлена определяется знаком коэффициента при наибольшей степени (или знаком свободного члена). Таким образом, критическая точка с координатами
. Как известно, квадратный трехчлен не меняет знак в том случае, если не имеет корней, то есть если его дискриминант отрицателен. В случае отрицательного дискриминанта знак квадратного трехчлена определяется знаком коэффициента при наибольшей степени (или знаком свободного члена). Таким образом, критическая точка с координатами 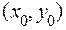 является точкой локального экстремума, если
является точкой локального экстремума, если 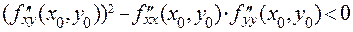 . При этом мы имеем точку минимума, если
. При этом мы имеем точку минимума, если 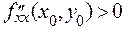 , и точку максимума, если
, и точку максимума, если 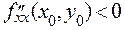 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Каскадное соединение согласованных | | | Локальный экстремум в случае функции трех и более числа переменных |
Дата добавления: 2014-03-03; просмотров: 489; Нарушение авторских прав

Мы поможем в написании ваших работ!