
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Оценка экономической эффективности ППП на стадии системного анализа предметной области
Проблемно-ориентированный ППП, функции которого многообразны и четко определены – достаточно крупная и дорогостоящая компонента любой информационной системы производственного назначения. Поэтому имеет смысл постановка вопроса об экономической эффективности отдельного ППП, вне рамок всей ИС.
В отличие от сложных проблем управления предприятием, очень часто трудноформализуемых, задачи оперативного управления производством связаны с огромными объемами рутинной работы и допускают, как правило, эффективную алгоритмизацию. Основной результат их решения с использованием современных машинных технологий, в частности ППП – это сокращение производственных потерь, перечень и порядок величин которых относительно просто устанавливаются на стадии обследования объекта внедрения пакета. Ясно, что чем выше степень детализации планирования и учета работы отдельных производственных единиц и различного рода вспомогательных служб, чем выше уровень синхронизации их функционирования, тем ниже потери от брака, простоев оборудования, штрафных санкций и т.п. В принципе, все производственные потери, происхождение которых зависит исключительно от качества оперативного управления объектом, т.е. степени детализации его описания и своевременности решения задач, могут быть сведены к нулю. Однако, как показывает опыт, достижение подобной цели на практике оказывается экономически нецелесообразным. Это принципиально важное утверждение, строго обоснованное академиком В.А.Трапезниковым (см.литературу к гл.V). Дело в том, что с ростом количества I обрабатываемых реквизитов, т.е. имен входных и выходных данных решаемых пакетом задач, объем и, следовательно, стоимость функционального и системного наполнения быстро увеличиваются. Одновременно резко усложняется проблема контроля достоверности входной и выходной информации пакета.
Покажем, что при весьма общих предположениях относительно зависимости эффективности Е от I, т.е. функции Е=Е(I), задача ее оценки допускает простое и полезное для практики решение. Прежде всего, в соответствии с основным назначением ППП, как это отмечено выше, будем считать, что его эффективность оценивается в денежном выражении как годовая экономия от исключения потерь. Если потенциально возможные потери составляют – Pmax, то предельная эффективность пакета будет Emax=½–Pmax½. Естественно предположить, что E(I) есть некоторая монотонно возрастающая функция, такая что с ростом I E(I)®Emax.
Далее пусть до внедрения ППП число обрабатываемых реквизитов составляло I0, a E(I)=E0 и потери P0=Emax-E0. Предположим, на этапе технико-экономического обоснования было признано целесообразным, разрабатывая новые задачи, увеличить число реквизитов до I+I0. Ясно, что прирост эффективности dE(I) должен быть пропорционален имеющемуся резерву ее повышения, иными словами, еще не устраненным потерям, т.е.
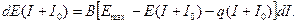 |
Причем, к потерям надо теперь отнести и затраты на обработку I+I0 по новой (пакетной) технологии, где q – годовая стоимость обработки одного реквизита.
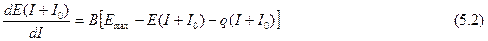 |
Перепишем последнее выражение в виде
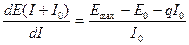 |
Для определения коэффициента пропорциональности В воспользуемся начальными условиями, из которых следует, что
при I=0.
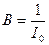 |
Таким образом,
и (5.2) в окончательном виде будет
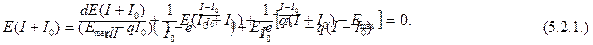 |
Единственным решением этого дифференциального уравнения является функция
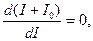 |
Нас интересует ее максимум. Решив уравнение
получим оптимальное значение I:
 |
Как следует из последнего выражения, для того, чтобы Iопт.>I0, необходимо выполнение неравенства
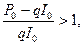
или, что одно и то же,
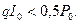
Это и есть критерий эффективности внедрения новых задач. Он означает, что если затраты на обработку I0 реквизитов с помощью ППП меньше половины имеющихся потерь, имеет смысл увеличение объема обрабатываемых данных. Для иллюстрации полученных результатов приведем один численный расчет. Примем, что Р0 = 0,1 Emax, т.е. эффективность на момент внедрения ППП составляла E0 = 0,9 Emax (90% от предельной ); qI0 = 0,4; P0 = 0,04 E max ( в соответствии с полученным критерием ). Так как прирост эффективности


то срок окупаемости ППП будет
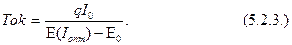
Сделав подстановку (5.2.2.) в (5.2.1.) и выразив все переменные (5.2.3.) через Emax, получим, что Ток » 1,5 года, а I опт » 1,4 I0.
В заключении заметим, что полученные аналитические зависимости не могут заменить конкретных экономических расчетов, связанных с разработкой (покупкой) пакета, однако они дают достаточно определенные ориентиры разработчикам и заказчикам при общей оценке перспективности подобных работ.
| <== предыдущая страница | | | следующая страница ==> |
| Опыт применения оптимизационных ППП в экономике | | | Научное ПО |
Дата добавления: 2014-03-04; просмотров: 415; Нарушение авторских прав

Мы поможем в написании ваших работ!