Объединение, пересечение, разность, разбиение

Определение 1.3.1. Объединение множества А и множества В есть множество С, составленное из элементов А вместе с элементами В. Обозначают это так: 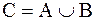. Объединение часто называется суммой множеств.

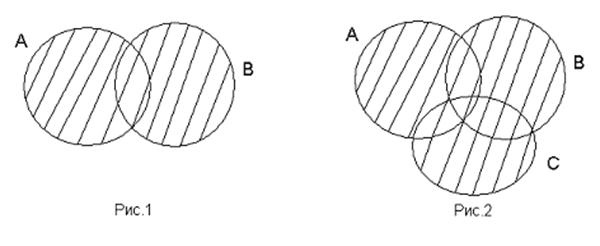
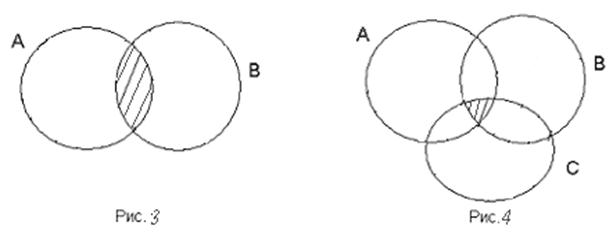
На рисунках 1 и 2 заштрихованные множества – это объединение двух и трех множеств. Такой способ изображения множеств и объединений множеств называется диаграммой Ванна.

Пример 1.3.1. Пусть А – множества всех курящих в какой-либо популяции, а В – множество отцов в этой популяции. Тогда 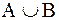- множество всех мужчин в популяции, которые являются либо курильщиками, либо отцами, либо и курильщиками и отцами одновременно.

Определение 1.3.2. Пересечение множества А и множества В есть множества С состоящее из элементов, принадлежащих множеству А и множеству В одновременно. Пересечение записывается как .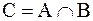

В диаграммах Венна пересечение любого числа множеств соответствует перекрыванию областей, представляющих сами множества.

Пример 1.3.2. Пусть А – множество особей в популяции плодовой мушки у которых имеется мутация крыльев, В – множество мушек с мутацией глаз. Тогда 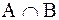- множество мушек с мутацией крыльев и глаз.

Определение 1.3.3. Два множества А и В называются непересекающимися, если они не содержат никаких общих элементов, т.е. .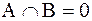

Пример 1.3.3. Пусть А – множество больных старше 30 лет, В – множество больных младше 20 лет. Тогда .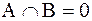

Определение 1.3.4. Разностью множеств А и В называется, состоящее из всех элементов А на входящих в В. Обозначают это так: 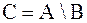. Чтобы получить разность 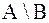достаточно удалить из множества А общие элементы множеств А и В т.е. множества .

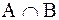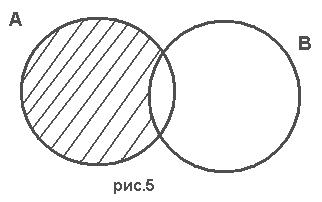
Пример 1.3.4. Пусть в некоторой популяции М – множество всех мужчин, а Т – множество всех людей, у которых туберкулез. Тогда М – женщины, Т –люди у которых нет туберкулеза.

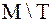- мужчины у которых нет туберкулеза,

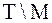- женщины с туберкулезом.

Определение 1.3.5.Разбиение множества А есть набор его подмножеств 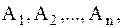которые взаимно не пересекаются и в объединении дают А. Это можно записать как

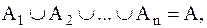
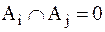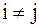при и .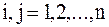

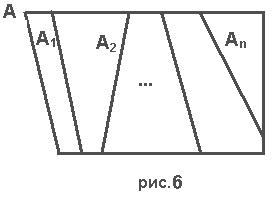
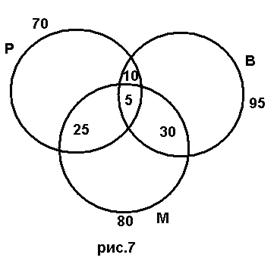
Пример 1.3.5. Из группы всю студентов, занимающихся естественными науками, 70 студентов посещают лекции по крайней мере одного курса физики, 95 ходят на биологию, 80 на математику. Предположим, что 30 студентов посещают и математику и физику, 35 математику и биологию, 15 физику и биологию. Предположим, что 5 студентов посещают лекции по всем трем предметам. Сколько студентов посещают лекции по всем трем предметам. Сколько студентов посещают лекции ровно по двум из этих трех предметов?

Решение: Определим Р, В и М как множества студентов, посещающих соответственно курсы по физике, биологии и математике. Тогда эти множества насчитывают 70, 95 и 80 студентов. Множества 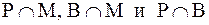соответственно содержит 30, 35, 15 элементов. Множество 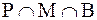- 5 элементов. Множество 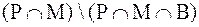содержит 30-5=25 элементов. Эти студенты изучают и математику и физику, но не биологию. Аналогично, 35-5=30 изучают только математику и биологию, 15-5=10 изучают только физику и биологию. Мы получаем, что ровно по двум из трех предметов занимаются 25=30=10=65 студентов.

Диаграмма Венна для этой задачи имеет вид:

Дата добавления: 2014-03-11; просмотров: 775; Нарушение авторских прав

Мы поможем в написании ваших работ!