Число перестановок, размещений, сочетаний

Определение 1.4.1.Перестановка из n объектов есть упорядочение этих объектов, т.е. расположение n объектов в определенном порядке.

Теорема 1.4.1.Число перестановок из n объектов есть n!, где

n!=1*2*3*…*n. ( 1.1)

Пример 1.4.1.Сколькими способами группа из шести человек может расположиться: 1) в ряд;

2) за круглым столом?

Решение.1) Искомым является число перестановок из шести объектов или 6!=1*2*…*6=720.

2) Чтобы расположить шестерых человек по кругу, выберем произвольно одного человека, а оставшихся пятерых упорядочим относительно выбравшего. Это можно сделать 5!=120 способами.

Определение 1.4.2.Перестановка из объектов по k( число размещений) есть любой выбор k объектов взятых в определенном порядке из n объектов. Обозначается это как .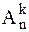

Теорема 1.4.2.Число размещений 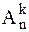есть

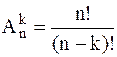(1.2)

Пример 1.4.2.Наконкурсе участвовало20 человек. Сколькими способами можно распределять первые три премии?

Решение.Искомоечисло способов есть число размещений из 20 объектов по три, т.е.

.

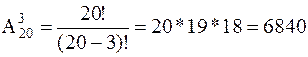Определение 1.4.3.Пусть у нас имеется множество из n объектов, содержащее 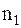объектов 1-го типа, 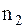- 2-го типа, … , 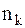- k-го типа, причем 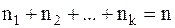. Определим полиномиальный символ 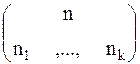как число перестановок из n объектов, среди которых 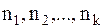являются неразличимыми.

Теорема 1.4.3.Справедлива формула

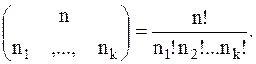(1.3)

Пример 1.4.3.Три типа бактерий культивируются в девяти пробирках. Три пробирки содержат бактерии 1-го типа, четыре – бактерии 2-го типа и две - - бактерии 3-го типа. Сколькими различными способами можно расположить пробирки в ряд на штативе, если нам важно расположение лишь типов бактерий?

Решение.Множество из девяти пробирок разбиваются на три подмножества, содержащие соответственно три, четыре и два неразличимых объекта. Тогда, .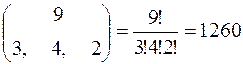

Определение 1.4.4.Число сочетаний 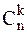из n объектов по k в каждом. Это любой выбор k объектов из n безотносительно к порядку выбора.

Теорема 1.4.4.Справедлива формула

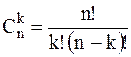(1.4)

Пример 1.4.4.У 6 мальчиков и 11 девочек в классе имеются признаки инфекционного заболевания. Чтобы проверить наличие заболевания, требуется взять выборочный анализ крови у двух мальчиков и двух девочек. Сколькими способами можно это сделать?

Решение.Существует 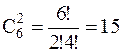способов выбора двух мальчиков и 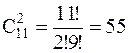способов выбора двух девочек. Тогда, число способов выбора двух мальчиков и двух девочек равно 15*55=825.

Пример 1.4.5.В лабораторной клетке имеется 8 белых и 6 коричневых мышей. Найти число способов выбора пяти мышей из клетки, если: 1) они могут быть любого цвета; 2) три из них должны быть белыми, а две – коричневыми; 3) они должны быть одного цвета.

Решение.1) В данном случае цвет не существенен. Поэтому имеется 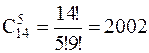способа, которыми 5 мышей можно выбрать из 14.

2) Существует способов выбора трех белых мышей и способов выбора двух коричневых мышей. Таким образом, имеется 56*15=840 способов выбора трех белых и двух коричневых мышей.

3) Существует 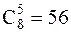способов выбора 5 белых и 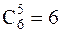способов выбора 5 коричневых мышей. Таким образом, имеется 56+6=62 способа выбора 5 мышей одинакового цвета.

Дата добавления: 2014-03-11; просмотров: 1335; Нарушение авторских прав

Мы поможем в написании ваших работ!