Множество, элемент множества, пустое множество

Лекция 1.Теория множеств.

Представление о множестве приводит к одному из самых общих понятий, которые встречаются в любой науке и в каждой области математики.

Множество – это любая четко определенная совокупность объектов. Предметы, составляющие множество, называют его элементами.Примерами множества могут служить: множество страниц данной книги (каждая страница является элементом этого множества), множество всех больных хирургического отделения больницы. То, что элемент a входит в множество A записывается так 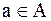( читается: a принадлежит множеству a ). Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Ǿ . Множество считается заданным, если указано некоторое свойство, которым обладают все его элементы и не обладают никакие другие объекты. Такое свойство множества называется характеристическим свойством. В зависимости от количества элементов составляющих множества они могут быть конечными или бесконечными. Например, множество всех натуральных чисел – бесконечно, а множество всех людей на Земле конечно.

1.2.Равенство множеств. Подмножество.

Универсальное множество. Дополнение множеств.

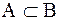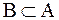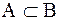Пусть A – множество элементов. Тогда B называется подмножеством A (обозначение ), если каждый элемент множества B является элементом множества A. Если и , то 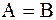. Каждое не пустое множество имеет по крайней мере два подмножества: пустое множество 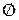и само множество A.

Пример 1.2.1.Пусть 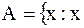- человеческое существо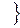и 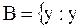- человеческое существо женского пола 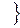. Тогда .

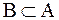Если выполнено условие 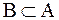и 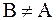то говорят, что B есть истинное (или собственное) подмножество A.

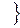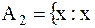Пример 1.2.2. Пусть - вид животных, - вид насекомых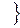и 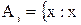- вид млекопитающих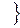. Тогда 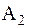и 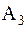являются истинными подмножествами .

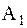Пусть нам дано какое – либо множество E. Мы будем рассматривать все возможные подмножества данного множества Е. Исходное множество Е в таком случае называют универсальным множеством. Пусть универсальное множество Е состоит из трех элементов 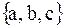. Перечислим все подмножества Е: 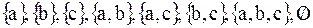. Их всего 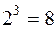подмножеств. Если универсальное множество Е состоит из n элементов, то число всех подмножеств множества Е равно .

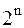Пусть А есть некоторое подмножество универсального множества Е. Тогда множество 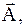состоящее из всех элементов множества Е не принадлежащих множеству А, называется дополнением множества А .

Пример 1.2.3. Пусть А – множество всех девочек группы. Тогда дополнением 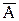является множество всех мальчиков той же группы.

1.3. Операции над множествами:

Дата добавления: 2014-03-11; просмотров: 729; Нарушение авторских прав

Мы поможем в написании ваших работ!