
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Виды соединения элементов в систему
1) Последовательное соединения.
2) Параллельное соединение.
1.17.1 Последовательное соединение элементов в систему
Соединение элементов называется последовательным, если отказ, хотябы одного элемента приводит к отказу всей системы. Система последовательно соединённых элементов работоспособна тогда, когда работоспособны все её элементы.
Рассчитаем надёжность системы при последовательном соединении элементов в систему. Рассчитать надёжность системы - это значит по заданным количественным характеристикам надёжности элементов определить количественные характеристики надёжности системы.
Рассмотрим события Ai, 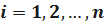 .
.
Событие Aiозначает безотказную работу элемента i за время t.
Считаем, что события Ai независимы, т.е. вероятность события AiP(Ai) не зависит от события Aj, 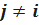 .
.
В этом случае элементы системы называются независимыми в смысле надёжности.
Рассмотрим событие A.
Событие A означает безотказную работу системы из n последовательно соединённых элементов за время t.
Событие A имеет место, если одновременно выполняются события Ai, 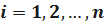 . Следовательно событие A равно произведению событий Ai, т.е.
. Следовательно событие A равно произведению событий Ai, т.е.
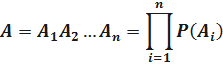
Обозначим 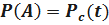 – вероятность безотказной работы системы за время t.
– вероятность безотказной работы системы за время t.
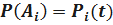 – вероятность безотказной работы i-го элемента за время t.
– вероятность безотказной работы i-го элемента за время t.
Откуда  .
.
Т.е., вероятность безотказной работы системы за время t равна произведению вероятностей безотказной работы за время t элементов системы.
В частном случае, когда все элементы системы одинаковы, имеем
 ;
;
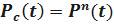 ;
;
Выразим вероятность безотказной работы элементов  через их интенсивность отказов
через их интенсивность отказов
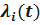 . Имеем
. Имеем
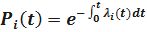 ;
; 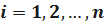
Запишем формулы для определения вероятности безотказной работы системы 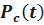 . Имеем
. Имеем
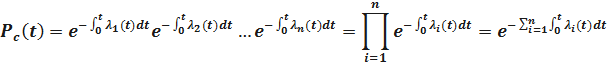
Или 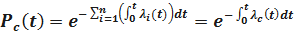
Где 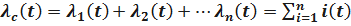
Здесь 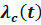 - интенсивность отказов системы.
- интенсивность отказов системы.
Т.е., при последовательном соединении элементов их интенсивность отказов складывается, и интенсивность отказов системы есть сумма интенсивностей отказов элементов системы.
Вероятность отказа системы на интервале времени (0, t) равна

Или 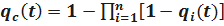 ;
;
Интенсивность отказов 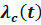 системы
системы
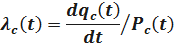
Среднее время безотказной работы системы

В случае экспоненциального закона надёжности всех элементов имеем:
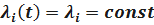 ;
;
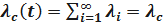 ;
;  ;
;
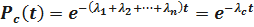 ;
;
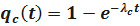 ;
;
 ;
;
Т.е. закон распределения времени безотказной работы системы является экспоненциальным.
Определим среднее время безотказной работы системы. Имеем
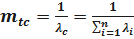 ;
;
| <== предыдущая страница | | | следующая страница ==> |
| Нормальный закон распределения | | | Параллельные соединения элементов в систему |
Дата добавления: 2014-08-09; просмотров: 677; Нарушение авторских прав

Мы поможем в написании ваших работ!